Вариант 8

1. В группе 10 студентов учатся на отлично, 12 - на хорошо и 8 - на удовлетворительно. Найти вероятность того, что наудачу вызванные два студента: а) учатся на "отлично", б) не учатся на "удовлетворительно".

2. Три стрелка стреляют в цель. Вероятность попадания в цель для первого, второго и третьего стрелка соответственно равна 0,6; 0,7 и 0,75. Определить вероятность хотя бы одного попадания в цель, если каждый стрелок сделает по одному выстрелу.

3. В первом ящике содержится 20 деталей, из них 15 стандартных, во втором - 30 деталей, из них 24 стандартных.

а) найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика - стандартная;

б) наудачу была извлечена стандартная деталь. Найти вероятность того, что эта деталь из первого ящика.

4. Стрелок производит по мишени 5 выстрелов. Вероятность попадания при каждом выстреле равна 0,4. Случайная величина Х -число попаданий в мишень при 5 выстрелах.

Найти:

а) закон распределения случайной величины X;

б) математическое ожидание М(х) и дисперсию D(x) случайной величины X;

в) наивероятнейшее значение случайной величины X.

5. На пути движения автомобиля 4 светофора, каждый из которых или разрешает дальнейшее движение или запрещает его с вероятностью 0,5. Случайная величина Х - число светофоров, пройденных автомобилем до первой остановки.

Найти:

а) закон распределения случайной величины X;

б) среднее значение случайной величины X.

Вариант 9

1. В квадрат со стороной "а" наудачу ставится точка. Определить вероятность попадания точки в круг, вписанный в квадрат.

2. Для сигнализации о пожаре установлены два независимо работающих датчика. Вероятность того, что при пожаре датчик сработа­ет, для первого и второго соответственно равны 0,9 и 0,95. Определить вероятность того, что при пожаре сработает а) только один датчик, б) хотя бы один датчик.

3. Имеется три одинаковые урны. В первой урне находятся 3 белых и 3 черных шара, во второй - 2 белых и 6 черных, в третьей - 5 белых и 2 черных. Из одной, наугад выбранной урны, взят шар.

а) найти вероятность того, что шар черный;

б) наугад взятый шар оказался черным. Найти вероятность того, что шар из второй урны.

4. Стрелок производит по мишени 5 выстрелов. Вероятность попадания при каждом выстреле равна 0,2. 3а каждое попадание стрелку засчитывают 10 очков. Случайная величина Х - число выбитых очков.

Найти:

а) закон распределения случайной величины X;

б) математическое ожидание М(х), дисперсию D(x) и среднее квадратическое отклонение (х) случайной величины X;

в) наивероятнейшее значение случайной величины.

5. На пути движения автомобиля 7 светофоров, каждый из которых или разрешает дальнейшее движение или запрещает его с вероятностью 0,5. Случайная величина Х - число светофоров, пройденных автомобилем до первой остановки.

Найти:

а) закон распределения случайной величины X;

б) среднее значение случайной величины.

Вариант 10

1. В коробке десять одинаковых, занумерованных кубиков. Наудачу извлекают один кубик за другим и выкладывают их в ряд. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.

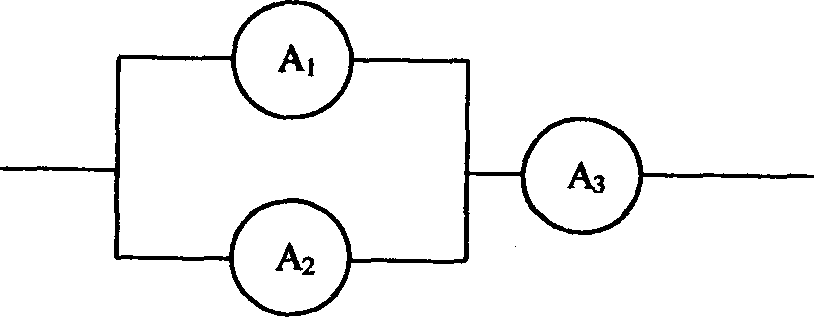
2. Определить вероятность выхода из строя электрической це­пи за данный промежуток времени, если вероятность выхода их строя элементов A₁; А₂; А₃ соответственно равна 0,6; 0,7 и 0,5.

3. Прибор может работать в двух режимах: А и В. Режим А наблюдается в 80% всех случаев работы прибора, режим В в 20% случа­ев. Вероятность выхода из строя прибора в режиме А равна 0,1; в режиме В - 0,7. а) найти вероятность выхода прибора из строя, б) прибор вышел из строя. В каком режиме, вероятнее всего, он работал?

4. Баскетболист забрасывает штрафной примерно с вероятностью 0,7. Баскетболист делает б штрафных бросков. Случайная величина Х - число попаданий. Найти:

а) закон распределения случайной величины X;

б) среднее значение числа попаданий;

в) среднее значение числа промахов.

5. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,4. Стрелку последовательно выдают патроны до тех пор пока он не промахнется. Случайная величина Х - число патронов, выданное стрелку до первого промаха.

а) составить закон распределения случайной величины X;

б) найти среднее ожидаемое число патронов, которые могут быть выданы стрелку.