МАТИ «РГТУ» им. Циолковского

Кафедра

«Электроника и информатика»

Курсовая работа по дисциплине

«Алгебра и геометрия»

	Выполнил: студент 1 курса группы 1ИНТ-1ВБ-048 Мельник Михаил Николаевич
	Преподаватель: Денисов Михаил Михайлович

Москва, 2012

Вариант № 9

1.1	Найти обратную матрицу……………………………………	3
1.2	Установить свойство ……………………	8
2.	Исследовать систему неоднородных линейных уравнений…………………………………………………......	12
3.1	Найти площадь треугольника:………………………………	17
3.2	С помощью скалярного произведения доказать, что вектор полученный от векторного произведения, перпендикулярен векторам и ………………………...	18
3.3	Определить компланарность векторов , какую тройку векторов образуют (правая, левая)…………………	19
4.	Задана прямая L и точка М .Требуется :
4.1	Вычислить расстояние q(M,L) от точки до прямой……….	20
4.2	Найти уравнение прямой L’, проходящей через точку М, и перпендикулярно заданной прямой L…………………….	21
4.3	Найти уравнение прямой L’’, проходящей через точку М, и параллельно заданной прямой L………………………….	22
4.4	Найти косинус угла (L1,L2) и точкой пересечения прямых.	23
5.1	Найти уравнение плоскости проходящей через точки M1 и M2 параллельную вектору …………………………………	25
5.2	Найти косинус угла между плоскостями ……...……	26

1.1 Найти обратную матрицу .

А=

Обратная матрица — такая матрица , при умножении на которую, исходная матрица A даёт в результате единичную матрицу E. Обратная матрица существует только для квадратных невырожденных матриц.

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Вырожденной называют квадратную матрицу, определитель которой равен нулю.

Нам дана квадратная матрица А, количество строк (четыре) равно количеству столбцов (четыре).

Найдем определитель матрицы А, для этого с помощью элементарных преобразований приведем матрицу к треугольному виду, после этого определитель будет равен произведению элементов главной диагонали.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц, например: перестановка местами любых двух строк матрицы, умножение любой строки матрицы на константу и прибавление (вычитание) этой строки к любой другой.

Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Определитель треугольной матрицы равен произведению элементов на её главной диагонали.

Умножим 1-ю строку на (-2) и вычтем полученную строку из строки 2

А=

Умножим 1-ю строку на (3) и вычтем полученную строку из строки 3

А=

Умножим 1-ю строку на (13) и вычтем полученную строку из строки 4

А=

Умножим 2-ю строку на (-2) и вычтем полученную строку из строки 3

А=

Умножим 2-ю строку на ( - ) и вычтем полученную строку из строки 4

А=

У множим 3-ю строку на (2) и вычтем полученную строку из строки 4

А=

Главная диагональ

Матрица приведена к треугольному виду, теперь перемножим все элементы главной диагонали и найдем определитель матрицы А.

Определитель равен 62. Он не равен нулю, значит наша матрица не вырожденная, т.е. мы можем найти обратную матрицу .

Следующий шаг – это составление присоединенной матрицы, состоящей из алгебраических дополнений.

Алгебраическим дополнением элемента матрицы А называется число:

,

где - дополнительный минор матрицы, получающейся из исходной матрицы путем вычёркивания i -й строки и j -го столбца.

Алгебраическое дополнение для элемента матрицы А:

Побочная диагональ

Здесь определитель вычисляется по правилу треугольника:

Перемножаем элементы главной диагонали, затем элементы, лежащие на параллелях к этой диагонали, и элементы из противолежащего угла. Далее сложим полученные элементы и вычтем элементы, полученные аналогичным путем, но относительно побочной диагонали.

Необходимо взять алгебраические дополнения для каждого элемента матрицы А.

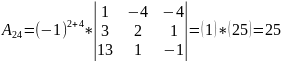
Вычислив все алгебраические дополнения, составим присоединенную матрицу , где алгебраическое дополнение соответствует элементу присоединенной матрицы, а индексы i и j у него обозначают строку и столбец в присоединенной матрице:

=

Теперь нам надо транспонировать полученную присоединенную матрицу :

Транспонировать матрицу – значит заменить строки столбцами и наоборот.

Чтобы получить обратную матрицу , нужно умножить полученную транспонированную присоединенную матрицу , на единицу деленную на определитель det A.

Чтобы умножить матрицу на число, нужно умножить каждый элемент матрицы на это число:

Мы получили обратную матрицу .