3.2.Проектирование кривошипно-ползунного механизма

3.2.1. Порядок расчета

Главный механизм проектируется по средней скорости ползуна (поршня). Рассматривается движение ползуна за один оборот кривошипа. Время одного оборота t_об=1/n, c. За это время путь, пройденный ползуном равен S_B=2H=4l₁,м средняя скорость ползун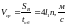а . Откуда .

Кроме того, спроектированный механизм должен удовлетворять ряду требований:

1. Рассчитанные размеры звеньев механизма должны обеспечивать проворачиваемость ведущего звена;

2. Механизм должен иметь минимальные размеры;

3. Для обеспечения наибольшего КПД и отсутствия заклинивания угол давления не должен превышать допустимого значения, т.е. должно выполняться условие .

В данном случае рассматривается центральный кривошипно-ползунный механизм, следовательно .

3.2.2. Синтез механизма и результаты расчета

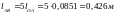
Проверка:

Для построения механизма необходимо выбрать масштаб Произвольно выбираем место расположения шарнира О, проводим через точку О вертикальную прямую. Кроме того, проводим из т. О окружность радиусом равным длине кривошипа ОА. Разобьем окружность через равные углы на 12 частей 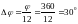. Полный цикл осуществляется за 1 поворот кривошипа. Из каждой точки вспомогательной окружностью радиусом равным АВ=170,4мм сделаем засечки на вертикали. Соединив полученные точки строим механизм в 12 положениях. Крайние положения точки В соответствуют ходу штока поршня Н=2l_OA.

3.3. Силы и моменты, действующие на звенья механизма.

Динамический анализ начинают с определения сил и моментов, которыми нагружен механизм, так как их характер определяет закон движения механизма. В данном случае задана индикаторная диаграмма и значения давления в цилиндре в зависимости от положения поршня.

Выбираем масштаб построения индикаторной диаграммы:

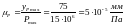
Сила F, действующая на поршень, является алгебраической суммой сил, действующих на поршень сверху (со стороны рабочей полости цилиндра) и снизу. Так как нижняя нерабочая полость цилиндра сообщается с атмосферой, то на поршень в любом положении механизма действует сила атмосферного давления и сила F будет пропорциональна ординатам, заключенным между линией атмосферного давления и соответствующей прямой индикаторной диаграммы.

Рассчитаем значения силы:

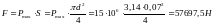
Выберем масштаб силы из условия равенства ординат графика давления и силы:

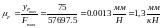
Учитывая чередование процессов, протекающих в цилиндре, строим график изменения силы в зависимости от положения входного звена. При этом масштаб по оси φ определиться следующим образом:

3.4.Определение параметров динамической модели

Для того чтобы упростить определение закона движения сложной системы, реальный механизм заменяют динамической моделью. Модель представляет собой стойку и вращающееся звено, называемое звеном приведения, инерционность которого определяется суммарным приведенным моментом инерции 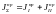. На звено приведения действует суммарный приведенный момент сил . Параметры динамической модели и 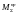определяют так, чтобы законы движения звена приведения динамической модели и движения реального механизма совпадали:

В качестве начального звена механизма выбран кривошип 1. Таким образом, обобщенная координата для механизма 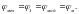и определяются методом приведения сил и масс.