
- •1. Задание на курсовую работу
- •1.2. Краткое описание работы.
- •1.2. Исходные данные
- •2.1.2. Постановка задачи:
- •2.1.3.Алгоритм расчета эвольвентной передачи:
- •2.1.4. Результаты расчета зубчатой передачи.
- •2.1.4. Выбор коэффициента смещения х1
- •2.1.6. Построение эвольвентного зубчатого зацепления.
- •2.1.7. Построение эвольвенты:
- •2.1.7. Станочное зацепление.
- •2.1.8. Графическая проверка коэффициента перекрытия:
- •2.1.9. Выводы:
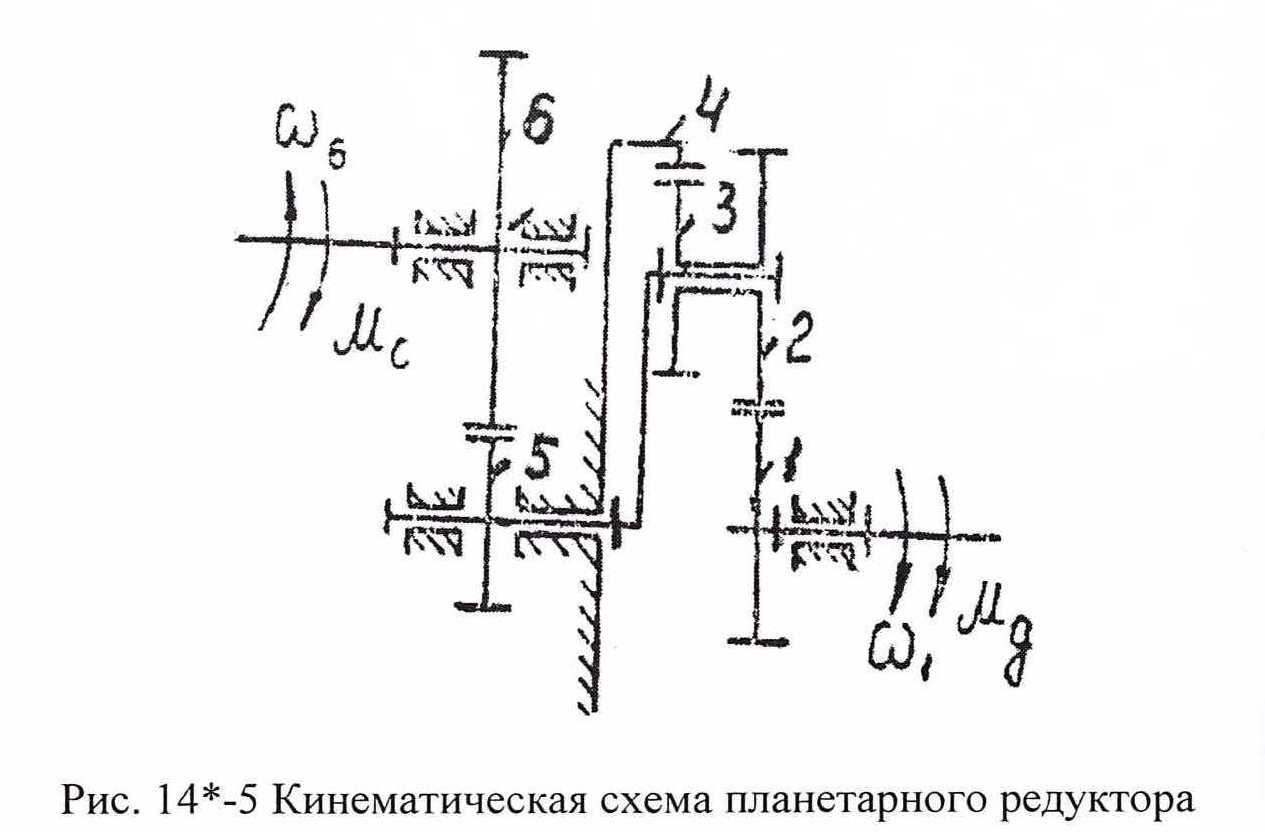
- •2.2 Проектирование планетарного редуктора.
- •2.2.1. Исходные данные:
- •2.2.2. Постановка задачи:
- •2.2.3. Основные условия накладываемые на многосателлитные редукторы:
- •2.2.4. Подбор чисел зубьев планетарного редуктора.
- •2.2.5. Графическая проверка передаточного отношения:
- •1. Расчет радиусов колес планетарного редуктора.
- •Проверка передаточного отношения из распределения линейных скоростей:
- •3. Проверка передаточного отношения из распределения угловых скоростей.
- •2.2.6 Выводы:
- •Лист II. Проектирование основного механизма и определение закона его движения
- •Исходные данные и постановка задачи
- •3.2.Проектирование кривошипно-ползунного механизма
- •3.2.1. Порядок расчета
- •3.2.2. Синтез механизма и результаты расчета
- •3.3. Силы и моменты, действующие на звенья механизма.
- •3.4.Определение параметров динамической модели
- •3.4.1. Определение суммарного приведенного момента
- •3.4.2. Определение суммарного приведенного момента инерции
- •3.5.Определение передаточных функций
- •3.6. Построение графика приведенного момента
- •3.7. Построение графика работы
- •3.8. Построение приведенного момента инерции второй группы звеньев
- •3.9. Построение приближенного графика
- •3.10. Расчет маховика
- •3.10.2. Определение момента инерции дополнительной маховой массы
- •3.11. Определение закона движения начального звена механизма
- •3.12. Выводы
- •4. Лист III. Проектирование кулачкового механизма
- •4.1.Исходные данные и постановка задачи
- •4.2.Построение кинематических диаграмм
- •4.3.Построение вспомогательной диаграммы
- •4.4.Профилирование кулачка
- •4.5.Проверка передаточных функций
- •4.5.1.Построение заменяющего механизма
- •4.5.2. Проверка передаточной функции скорости
- •4.5.3. Проверка передаточной функции ускорения.
- •4.6. Выводы.
- •5. Список литературы.
2.1.8. Графическая проверка коэффициента перекрытия:

 <
5%
<
5%
где
 - линия
зацепления, мм;
- линия
зацепления, мм;
 -
шаг по основной окружности, мм.
-
шаг по основной окружности, мм.
Правильность построения станочного зацепления:
Δymчерт = 3.02 мм
Δy = 0.765 мм
 <
5%, где
<
5%, где
Δy-коэффициент уравнительного смещения;
Δymчерт - уравнительное смещение полученное построением.
2.1.9. Выводы:
Выполнили геометрический расчет эвольвентной зубчатой передачи при нарезании колес инструментом со стандартным реечным исходным контуром, выбран коэффициент смещения
 ,
удовлетворяющий качественным показателям
передачи и обеспечивающий отсутствие
подреза и заострения. Распечатка
прилагается.
,
удовлетворяющий качественным показателям
передачи и обеспечивающий отсутствие
подреза и заострения. Распечатка
прилагается.Построена схема станочного зацепления при нарезании колеса с меньшим числом зубьев в
 .
.
Вычерчена схема зацепления колес с указанием основных размеров и элементов колес и передачи в .
Проверен коэффициент перекрытия графическим методом, погрешность
 .
.
2.2 Проектирование планетарного редуктора.
2.2.1. Исходные данные:
Схема – двухрядный планетарный редуктор со смешанным зацеплением;
U1В = U16
 =24
=24 =16;
=16;Число блоков сателлитов к = 3;
m=1 мм; х=0.
2.2.2. Постановка задачи:
Подобрать числа зубьев по заданному передаточному отношению и числу сателлитов. Допустимое отклонение передаточного отношения ±5%. Колеса планетарного редуктора нулевые; модуль колес принять равным единице.
Построить треугольники линейных скоростей и план угловых скоростей звеньев спроектированного редуктора.
Проверить передаточное отношение редуктора графическим способом.
2.2.3. Основные условия накладываемые на многосателлитные редукторы:
Обеспечение передаточного отношения планетарного редуктора, которое определяется по формуле Виллиса
 ,
,
где
 - передаточное отношение обращенного
механизма. Читается условие следующим
образом: передаточное отношение
планетарного редуктора от колеса 1 к
водилу равно 1 минус передаточное
отношение обращенного механизма от
колеса 1 к опорному 0.
- передаточное отношение обращенного
механизма. Читается условие следующим
образом: передаточное отношение
планетарного редуктора от колеса 1 к
водилу равно 1 минус передаточное
отношение обращенного механизма от
колеса 1 к опорному 0.
Условие соосности входного и выходного валов механизма, т.е. межосевое расстояние первой передачи должно быть равно межосевому расстоянию второй передачи
 .
.
Условие сборки, т.е. условие размещения сателлитов с равными углами
 между их осями (
между их осями ( ).
Математически это условие может быть
записано так:
).
Математически это условие может быть
записано так:
 ,
,
где z1-число зубьев солнечного колеса,
К – число сателлитов,
Р – целое число полных оборотов водилы,
N – любое целое число.
Условие совместности или соседства, которое учитывает возможность свободного размещения сателлитов без соприкосновения их друг с другом. Это условие будет выполнено, если расстояние между осями сателлитов будет больше диаметра окружности вершин сателлитов.
Математически это условие для механизмов записывается неравенством:

2.2.4. Подбор чисел зубьев планетарного редуктора.
Найдем передаточное отношение планетарного редуктора.

При подборе чисел зубьев учитываем ограничение накладываемое условием отсутствия подреза:
 внешнее
зацепление
внешнее
зацепление
 внешнее
зацепление
внешнее
зацепление
 внутреннее
зацепление
внутреннее
зацепление
Подбираем числа зубьев учитывая все условия накладываемые на многосателлитные редукторы.
Ограничение накладываемое условием сборки.


при любом p; z1 кратно 3.
1 и 2 условие решаем совместно методом неопределенных коэффициентов

(А+В)α= β
β
α= ;
β=(А+В)γ
;
β=(А+В)γ
 +
+ =
= -
-







соостность:

18+90=162-54
108=108
Условие соосности выполняется.
Проверим условие соседства:


Условие соседства выполняется.




