1. Матрицы, виды матриц, операции над матрицами (сложение, умножение на число, транспонирование, умножение матриц)

Матрицей размерности m x n называется прямоугольная таблица m x n чисел a _ij , i=1,..., m, j=1,..., n:

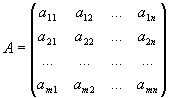
расположенных в m строках и n столбцах. Матрица называется квадратной, если m=n (n - порядок матрицы).

Линейные матричные операции По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы. Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

Произведение матриц определяется следующим образом. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если

, ,

то произведением матриц A и B, называется матрица

,

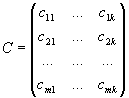элементы которой вычисляются по формуле

c ij = a i1 b 1j + a i2 b 2j + ... +a in b nj , i=1, ..., m, j=1, ..., k.

Произведение матриц A и B обозначается AB

, т.е. C=AB.

2. Определитель матрицы. Свойства определителей

Определителем квадратной матрицы (det A) называется число, которое может быть вычислено по элементам матрицы по формуле:

, где М_1k - определитель матрицы (детерминант), полученной из исходной матрицы вычеркиванием первой строки и k - oго столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов. Первая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя матрицы по первому столбцу:

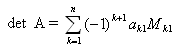
Вообще говоря, определитель матрицы может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:

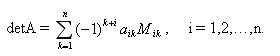
1. Если квадратная матрица A^T является транспонированной матрицей A, то их определители совпадают |A^T | = |A|, т.е. определитель не меняется, если заменить его строки столбцами и обратно, например, для определителя третьего порядка .

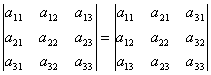Доказательство проводится проверкой, т.е. сравнением обеих частей записанного равенства. Вычислим определители, стоящие слева и справа:

2. При перестановке 2-х строк или столбцов определитель изменит знак на противоположный, сохраняя абсолютную величину, т.е., например,

Доказательство проводится аналогично доказательству свойства 1 сравнением обеих частей. Проведём его для определителя второго порядка.

.

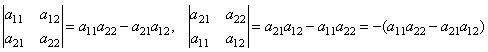Для определителя третьего порядка проверьте самостоятельно.

3. Если определитель имеет две одинаковые строки или столбца, то он равен нулю. Например, .

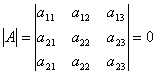Действительно, если переставить здесь 2-ю и 3-ю строки, то по свойству 2 этот определитель должен изменить знак, но сам определитель в данном случае не меняется, т.е. получаем |A| = –|A| или |A| = 0.

4. Общий множитель строки или столбца можно выносить за знак определителя. Например, .

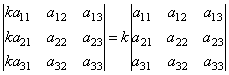Доказательство проводится проверкой, как и свойство 1. (Самостоятельно)

5. Если все элементы какой–либо строки или столбца определителя равны нулю, то сам определитель равен нулю. (Доказательство – проверкой).

6. Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,

.

Доказательство - проверкой, аналогично свойству 1.

7. Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины. Например,

.

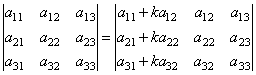Докажем это равенство, используя предыдущие свойства определителя.