Занятие 3
1. Задача оптимального распределения инвестиций по проектам
Словесная формулировка. Имеется ряд проектов, намеченных к реализации в течение некоторого периода. По каждому проекту задан график возврата средств, выделяемых на его реализацию, представленный в виде последовательности коэффициентов возврата, выражающих собой долю взятого кредита, которую необходимо вернуть кредитору в указанное время. Требуется найти распределение средств по проектам, приносящее максимальный доход за инвестиционный период. Для решения таких задач используются линейные динамические модели.
Формальная
постановка. Пусть инвестиционный
период разбит на m
временных интервалов, следующих
непосредственно один за другим;
и
–
объем инвестиций в j-й
проект и их предельное значение
соответственно;
коэффициент
возврата этих инвестиций в начале i-го
интервала. Пусть средства инвестора
хранятся в банке с коэффициентом
доходности ki
за i-й интервал.
Тогда остатки
и
на банковском счете инвестора в начале
и конце i-го периода
будут равны:
;
;
,
,
(1.1)
где H – величина средств инвестора в начале инвестиционного периода.
Остатки на начало m-го интервала следует максимизировать:
. (1.2)
Соотношение
(1.1) вместе с рекуррентными соотношениями
(1.2), описывающими динамику изменения
средств инвестора, условиями
и
,
представляют формальную постановку
задачи.
Задача 1.1. Компания, желая оптимальным образом использовать имеющиеся у нее денежные средства, разрабатывает оптимальный план инвестиций на ближайшие пять лет. На выбор у компании имеется пять инвестиционных проектов, параметры денежных потоков которых представлены в следующей таблице
-
Год
Проект А
Проект В
Проект С
Проект D
Проект Е
1
-1
0
-1
-1
-1
2
0,7
-1
0,2
-1
0
3
0,1
0,1
0,6
0,5
0,1
4
0,1
0,1
0,4
0,9
0,6
5
1,6
2
1,6
2,5
1,6
Участие в инвестиционном проекте «С» обязательное и требует не менее 6,9 млрд. руб., а проект «В» не допускает инвестиций более 6,2 млрд. руб. Размер имеющихся у компании денежных средств на момент планирования инвестиций составляет 14 млрд. руб.
Определить размеры инвестиций в каждый проект, обеспечивающие максимальную отдачу.
Решение. В соответствии с формализацией (1.1)-(1.2) остатки и на банковском счете инвестора в начале и конце i-го года будут равны:
;
;
,
,
Остатки в конце периода следует максимизировать:
Добавляя
условия
,
,
,
получаем и решаем задачу с помощью
надстройки «Поиск решения» Excel:
1) отводим блок ячеек под искомые размеры инвестиций (ячейки B10:F10 на шаблоне, рис.1 ниже);
2) считаем обороты (G3:G7) и остатки денег (H3:H7) на р/с компании для каждого года;
3) ставим задачу в «Поиске решения» и решаем ее.
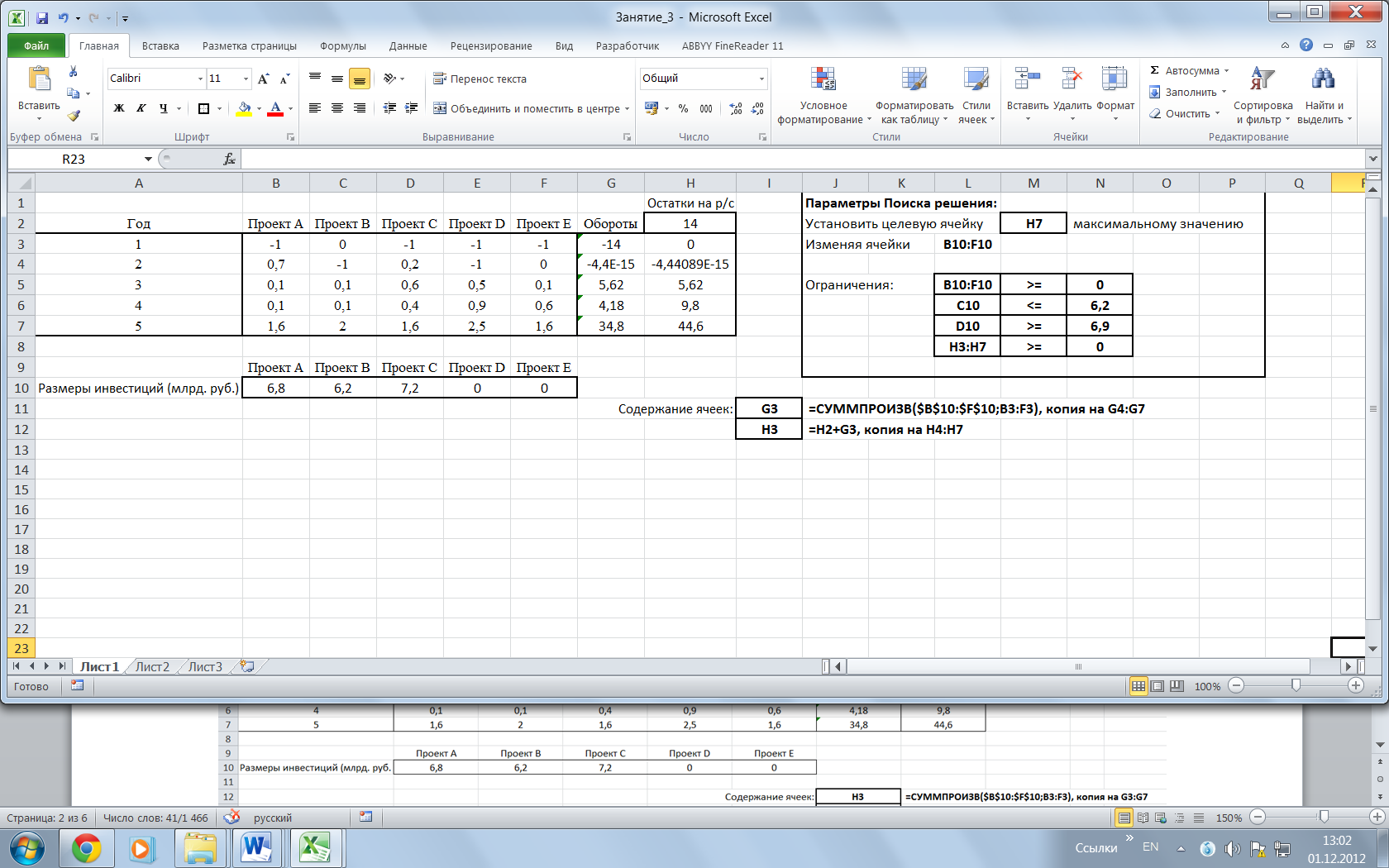
Рис 1. Шаблон с решением задачи 1.1
Задача 1.2. Представители пяти проектов конкурируют между собой за получение кредита. Графики потока платежей погашения кредитов представлены в таблице:
-
Год
Проекты
A
B
C
D
E
1
-1,0
0
-1,0
-1,0
0
2
+0,3
-1,0
+1,0
0
0
3
+1,0
+0,3
0
0
-1,0
4
0
+1,0
0
+1,75
+1,4
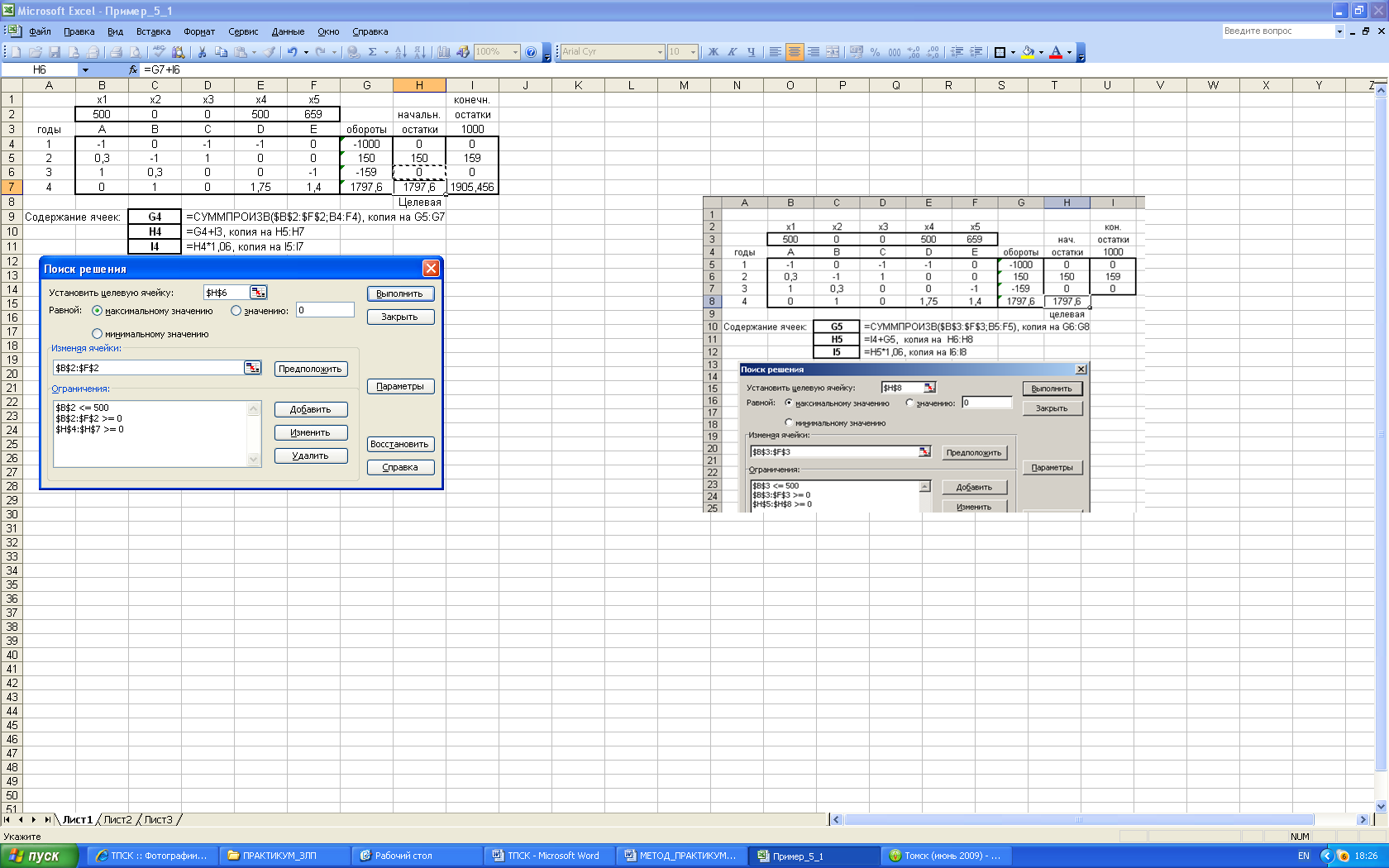
Например, проект А стартует в начале первого года сразу после получения кредита; в начале второго года возвращает инвестору 0,3 от всей взятой суммы; в начале третьего года (момент окончания проекта) взятые деньги возвращаются с коэффициентом 1. Проект В аналогичен проекту А, но начинается на год позже. И так далее. Доходы, полученные от текущих проектов, можно направить в другие. Средства инвестора хранятся на банковском счете с доходностью 6% годовых. Максимальная сумма, требуемая для проекта А, равна 500 у.е. По другим проектам объем вложений не ограничен. В начальный момент у инвестора имеется 1000 у.е. Найти оптимальные объемы инвестиций в проекты, обеспечивающие максимальный доход инвестора к началу 4-го года периода.
Решение. В соответствии с формализацией (1.1)-(1.2) остатки и на банковском счете инвестора в начале и конце i-го года будут равны:
;
;
,
,
Остатки на начало 4-го года периода следует максимизировать:
Добавляя условия
,
;
получаем задачу и решаем ее с помощью
надстройки «Поиск решения» Excel:
|
|
Рис. 1.2. Шаблон с решением задачи 1.2