25. Перерізи циліндра і конуса площиною.

1.

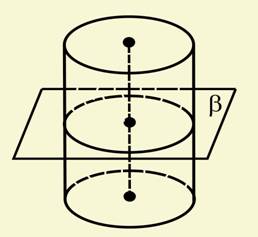
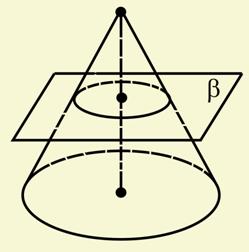
2.

26. Перерізи тіл обертання.

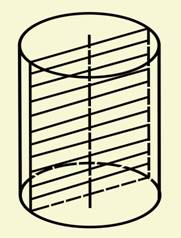
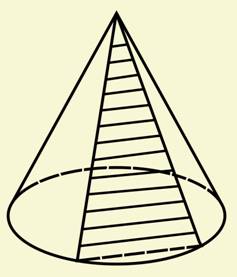
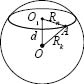
На рисунку у , OA — радіус кулі, — радіус перерізу, — відстань від центра кулі до площини перерізу (d). .

27. Куля та сфера.

Кулею називається тіло, що складається з усіх точок простору, які розташовані від даної точки на відстані, що не більша за дану. Ця точка називається центром кулі, а дана відстань — радіусом кулі. Межа кулі називається кулевою поверхнею, або сферою. Відрізок, що сполучає дві точки кульової поверхні й проходить через центр кулі, називається діаметром. Куля є тілом обертання, яке утворюється під час обертання півкруга навколо його діаметра як осі.

Сфера-Це фігура, що складається із всіх крапок простору, вилучених від даної крапки на даній відстані.

28. об’єми тіл оберт та пл. їх поверхонь: циліндра

Об’єм циліндра (див. рисунок) дорівнює добутку площі його основи та висоти. ; .

Площа бічної поверхні циліндра обчислюється за формулою S = 2pRh, де R — радіус циліндра, h — висота циліндра.

Площа повної поверхні циліндра обчислюється за формулою S = 2pR(R + h), де R — радіус циліндра, h — висота циліндра.

29. об’єми тіл оберт та пл. їх поверхонь: конуса

Об’єм конуса дорівнює одній третині добутку площі його основи та висоти. . .

Об’єм зрізаного конуса

Площа бічної поверхні конуса обчислюється за формулою S = p Rl, де R — радіус основи конуса, l — висота твірної.

Площа повної поверхні конуса обчислюється за формулою S = p R(R + l), де R — радіус основи конуса, l — висота твірної.

30. об’єми тіл оберт та пл. їх поверхонь: кулі.

Об’єм кулі: , де R — радіус кулі.

Площа сфери обчислюється за формулою: S = 4pR², де R — радіус сфери.

31. розбиття тіл на простіші, вимірювання параметрів реальних тіл та їхніх фізичних моделей.

32. функції, їхні властивості графіки.

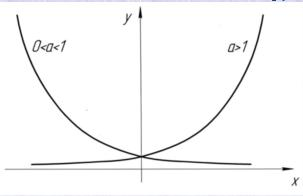
Властивсті і графіки показникової функції

1. Область визначення функції a^x – множина R дійсних чисел. 2. Область значень функції a^x (якщо a≠1) – множина R₊ всіх додатних дійсних чисел. Якщо a=1, функція a^x при всіх x стала: вона дорівнює 1. 3. Якщо a>1, функція a^x зростає на всій числовій прямій; якщо 0<a<1, функція a^x спадає на множині R.

Логарифми та іх властивості.

Число називається логарифмом числа за основою , якщо

Логарифм добутку двох чисел дорівнює сумі логарифмів цих чисел:

Різниця логарифмів дорівнює логарифму дробу:

дозволяє переходити від одної основи до іншої,

,

.

а також:

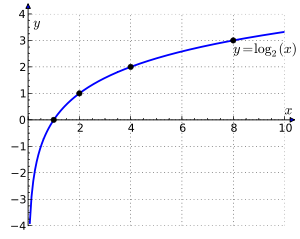
Графік функції log₂(x) проходить через точки з координатами (1, 0); (2, 1); (4, 2); (8, 3). log₂(2) = 1, тому що 2¹ = 2, log₂(4) = 2, тому що 2² = 4, log₂(8) = 3, тому що 2³ = 8

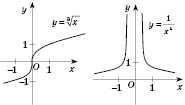
Степеневі функції

 Степенева функція з натуральним показником - функція, задана формулою  де n - натуральне число.

При n=1 одержуємо функцію y=x, її властивості розглянуті на сторінці «Лінійна функція»

При n=2;3 одержуємо функції   , :

  Нехай n - довільне парне число, більше двох: 4,6,8...   У цьому випадку функція y=xn має ті ж властивості, що і квадратична функція (див. сторінку сайту «Квадратична функція»).    Графік функції нагадує параболу , тільки вітки графіка при |х|>1 тим крутіше йдуть вгору, чим більше n, а при |х|<1 тим «тісніше притискаються» до осі Х, чим більше n.

  Нехай n - довільне непарне число, більше трьох: 5,7,9... У цьому випадку функція має ті ж властивості, що і функція .   Графік функції нагадує кубічну параболу.

Область визначення: при a < 0, при a > 0.

При натуральних показниках степеня a область визначення розширюєтья на всю числову вісь: .

Область значень: при a < 0, при a > 0.