1. Елементи комбінаторики.

Предмети, з яких складається множина наз. її елементами. Множини бувають скінченні й нескінченні. Комбінаторика – розділ математики, в якому вивчаються методи розв’язування комбінаторних задач. Дві множини називаються рівними, якщо вони складаються з тих самих елементів. Перерізом множин А і В наз множина С, яка складається х усіх тих і лише тих елементів, які належать кожній з даних множин А і В. Об’єднанням двох множин А і В наз така множина С, яка складається з усіх елементів множин А і В і лише з них. Різницею двох множин А і В наз така множина С яка складається з усіх елементів множини А які не належать множині В.

2. Перестановки, розміщення, комбінації.

Кожну з двох упорядкованих множин наз перестановкою з трьох елементів. Будь-яка впорядкована множина яка складається з n елементів, наз перестановкою з n елементів.

Будь-яка впорядкована підмножина з n елементів даної множини М, яка містить m елементів, де n≤m, наз розміщенням з m елементів по n.

Будь-яка впорядкована підмножина з n елементів даної множини М, яка містить m елементів наз комбінацією з m елементів по n.

3. Стохастичний експеримент і випадкова подія.

Будемо називати експеримент стохастичним якщо за виконанням певної сукупності умов його можна повторювати необмежену кількість разів і результати якого наперед не можна передбачити. Подію наз випадковою якщо за виконанням певної сукупності умов S вона може відбутися або не відбутися.

4. Відносна частота події.

Нехай деяке випробування вироблено n разів і в результаті цього пов'язане з ним випадкова подія (позначимо його через А) відбулося k разів. Тоді відносної частотою випадкової події А, назвемо ставлення k до n . Іншими словами .

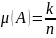?5. Операції над подіями.

???

6. Ймовірність події.

Випадковим подіям ставлять у відповідність певне число яке тим більше чим більш можлива подія ( чим більше у неї шансів відбутися). Таке число наз імовірністю події. Ймовірність є числова міра її об’єктивної можливості відбутися. Ймовірність – числова характеристика можливості появи випадкової події за певної умови яку можна відтворити необмежену кількість разів.

7. Ймовірність суми та добутку подій.

Імовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій, тобто P(A+B) = P(A)+P(B).

Імовірність спільної появи двох незалежних подій дорівнює добутку імовірностей цих подій тобто P(AB)=P(A)*P(B)

8. Дискретна випадкова величина, закон її розподілу.

Дискретною випадковою величиною називається випадкова величина, що приймає скінчене число значень з множини, елементи якої можна пронумерувати. Законом розподілу дискретної випадкової величини називають відповідність між можливими значеннями і їх імовірностями. Його задають таблично , графічно чи аналітично (у виді формул). Сума імовірностей закону розподілу дорівнює 1.

9. Математичне сподівання дискретної випадкової величини.

Математичним сподіванням дискретної випадкової величини називають суму добутків всіх її можливих значень на їх імовірності.

10. Вибіркові характеристики.

Вибіркове спостереження є найбільш поширеним видом несуцільного спостереження. При цьому обстеженню підлягає не вся статистична сукупність, а лише її певна частина, яка відбирається за відповідними правилами та представляє сукупність в цілому. Вибіркове спостереження має суттєві переваги порівняно з суцільним: воно є більш оперативним, вимагає менше коштів та часу на підготовку та проведення. Вибіркові характеристики :

n – чисельність вибіркової сукупності;

х – середнє значення ознаки у вибірковій сукупності ( вибіркова середня );

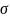2 – дисперсія;

W – вибіркова частка ;

2w – дисперсія альтернативної ознаки 2w = W (1-W).

?11. Закон великих чисел. Вибірковий метод у статистиці.

Теорема Бернуллі є простішою формою закону великих чисел.

Теорема. Якщо в ряді випробувань імовірність деякої події залишається для кожного випробування сталою, то з достовірністю можна стверджувати, що при досить великій кількості випробувань статистична частота цієї події відрізнятиметься як завгодно мало від її імовірності.

?12. Зміст середніх показників, оцінка числових характерних випадкової величини за її вибірковими характеристиками.