Глава 2. Основная теорема симплекс-метода.

Если после выполнения очередной итерации:

1. Найдется хотя бы одна отрицательная оценка ∆_s ˂0, и в каждом столбце с такой оценкой будет хотя б один положительный элемент ∆_is >0, то решение можно улучшить, выполнив следующую итерацию;

2. Найдется хотя б одна отрицательная оценка ∆_s ˂0, столбец которой не содержит положительных элементов, т.е. все ∆_is ≤0 ( ), то целевая функция Z неограниченна в области допустимых решений, т.е. Z_max→∞;

3. Все оценки ∆_j ≥0 ( 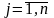),то получено оптимальное решение. Решение конкретных ЗЛП будем проводить в таблицах, аналогично таблицам Гаусса, которые называются симплексными (или сиплекс-таблицами).

Доказательство.

1. Выберем разрешающий элемент согласно пп. (1)-(3) теоремы и перейдем к новому опорному решению Х₁ , для которого значение Z(Х₁) больше, чем Z₀ , на величину «-∆_sx_s»>0. Следовательно, новое опорное решение будет лучше предыдущего.

2. Пусть ∆_s ˂0 и все ∆_is ≤0 ( ). Тогда, если переменную х_s ввести в базис, функция Z увеличится на величину ∆Z=-∆_sx_s >0.

При наличии а_is >0 величина х_s ограничивается минимумом отношений b_i/ а_is для а_is >0. Если же все а_is ≤0, то значение х_s можно не ограничивать, так как при любом сколь угодно большом значении х_s значения всех остальных базисных переменных х_i всегда будут неотрицательными, поскольку

х_i=b_i-a_isx_s и при а_is ≤0 значения х_i всегда положительны. Таким образом, переменной х_s можно придавать сколь угодно большое значение, при этом целевая функция Z будет достигать тоже сколь угодно большого значения, т.е. Z_max→∞.

3. Если все оценки ∆_j ≥0, то увеличивая любую свободную переменную, мы будем уменьшать значение целевой функции Z. Отсюда вытекает, что ни при каком другом допустимом решении функция Z не может быть увеличена, т.е. найденное решение является оптимальным. Теорема доказана.

Глава 3. Практика.

Швейная фабрика выпускает платья двух моделей А и В, использует для этого ткань двух видов и рабочее время. Затраты ткани каждого вида, рабочего времени на изготовление одного платья, соответствующая прибыль, а также запасы ткани и рабочего времени даны в таблице:

Ресурсы	Затраты ресурсов на изготовление 1 платья модели			Наличие ресурсов
	А	В
Ткань 1 вида (м)	4	0	500+20N
Ткань 2 вида (м)	2	4	1200+30N
Раб. время (чел/час)	8	4	1292+60N
Прибыль (у.е.)	10	2,5	N=13

Определить, сколько платьев модели А и В надо выпустить, чтобы получить максимальную прибыль.

3.1 Решение злп графическим методом.

Пусть швейная фабрика выпускает х₁ платьев модели А и х₂ платьев модели В. Тогда на все изделия будет затрачено 4х₁+0۰х₁ ткани 1 вида, 2х₁+4х₂ ткани 2 вида и 8х₁+4х₂ рабочего времени. Прибыль составляет 10х₁+2,5х_2.

Учитывая условия задачи, получаем математическую модель

х₁ ≥0, х₂ ≥0;

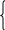4х₁ ≤ 760

2х₁+4х₂≤1590

8х₁+4х₂≤2072

Z = 10х₁+2,5х₂→max

Решение:

Запишем уравнения граничных прямых:

1). 4х₁ =760, х₁ =190;

2). 2х₁+4х₂ = 1590,

х1	0 795
х2	397,5 0

3). 8х₁+4х₂ = 2072,

х1	0 259
х2	518 0

В ыберем удобный масштаб, ориентируясь на найденные точки. Построим эти три прямые, видим, что областью решений ЗЛП является пересечение всех полуплоскостей – многоугольник ОАВСD. Строим вектор N=(10;2,5) и через начало координат линию уровня МР, перпендикулярную вектору N. Передвигая линию МР параллельно самой себе в направлении вектора N, находим точку максимума функции Z – точку С. Ее координаты найдем, решив систему уравнений:

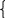4х₁ ≤ 760 х₁ =190

8х₁+4х₂≤2072 х₂ =138

С=(190, 138).

Вычисляем Zmax =Z(С)=10*190+2,5*138=2245.

Ответ: чтобы получить максимальную прибыль 2245 у е швейная фабрика должна выпустить 190 платьев модели А и 138 платьев модели В.