ПЛАН.

Ведение.

Глава 1. Свойства решений злп.

1. Теорема 1. О выпуклости множества планов ЗЛП.

2. Теорема 2. О достижении целевой функцией ЗЛП оптимального значения в угловой точке многогранника решений.

3. Теорема 3. О соответствии опорному плану ЗЛП угловой точки ее многогранника решений.

4. Теорема 4. О соответствии угловой точке многогранника решений ЗЛП ее опорного плана.

Глава 2. Основная теорема симплекс-метода.

Глава 3. Практика.

3.1 Решение ЗЛП графическим методом.

3.2 Решение ЗЛП симплекс-методом.

3.3 Сравнительная характеристика результатов симплексного и графического метода решений.

Использованная литература.

ВВЕДЕНИЕ.

Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения.

Наиболее простым и наглядным методом линейного программирования является графический метод. Он применяется для решения ЗЛП с двумя переменными. Если переменных больше двух, то применяется симплексный метод решения ЗЛП.

Симплекс-метод был разработан американским ученым Джорджем Данцигом в начале 50-х годов ХХ столетия. Он состоит из двух этапов (шагов):

1. Нахождение исходного опорного решения ЗЛП;

2. Нахождение оптимального решения. Этот этап носит название симплекс-алгоритм.

Таким образом, целью реферата является:

1. изучить теоретические сведения, необходимые для решения ЗЛП. Т.е. сформулировать и доказать теоремы графического и симплексного метода решения ЗЛП.

2. решить данную ЗЛП графическим и симплексным методом, сделать их сравнительный анализ.

Глава 1. Свойства решений злп.

1. Теорема 1. О выпуклости множества планов злп.

Множество планов (решений ) ЗЛП выпукло.

Доказательство:

Рассмотрим ЗЛП в матричной форме:

Х≥0;

А۰Х=В;

Z=C۰Х max.

Необходимо доказать, что если Х₁,Х₂ – планы ЗЛП, то их выпуклая линейная комбинация

Х=λ₁Х₁ + λ₂Х₂;

λ₁ + λ₂ = 1;

λ₁ ≥0; λ₂ ≥0;

также является планом задачи.

Поскольку Х₁,Х₂ – планы задачи, то выполняются соотношения:

АХ₁=В, Х₁ ≥0;

АХ₂=В, Х₂ ≥0.

Перемножая А۰Х=А(λ₁Х₁ + λ₂Х₂)= λ₁АХ₁ + λ₂АХ₂ = λ₁В + λ₂В= (λ₁ + λ₂)В=В, получаем, что Х удовлетворяет условию А۰Х=В. Но так как Х₁ ≥0, Х₂ ≥0, λ₁ ≥0, λ₂ ≥0, то и Х ≥0, т.е. удовлетворяет условию Х≥0. Таким образом, Х является планом ЗЛП.

2. Теорема 2. О достижении целевой функцией злп оптимального значения в угловой точке многогранника решений.

Целевая функция ЗЛП достигает своего оптимального значения в угловой точке многогранника решений ЗЛП. Если целевая функция достигает оптимального значения в нескольких угловых точках, то она достигает оптимального значения в любой точке, являющейся выпуклой линейной комбинацией этих угловых точек.

Доказательство:

Рассмотрим ЗЛП на максимум в матричной форме:

Х≥0;

А۰Х=В;

Z=C۰Х max.

Предположим, что многогранник решений является ограниченным, имеющим конечное число угловых точек. Обозначим его через D. В двумерном пространстве D имеет вид многоугольника, изображенного на рис.

Обозначим угловые точки многогранника Dчерез Х₁,Х₂,…,Х_p, а оптимальный план - через Х₀ . Тогда Z(Х₀)≥Z(Х) для всех Х из D. Если Х₀ – угловая точка, то первая часть теоремы доказана.

Допустим, что Х₀ не является угловой точкой. Тогда Х₀ можно представить как выпуклую линейную комбинацию угловых точек многогранника т.е.

Х₀ = λ₁Х₁ + λ₂Х₂+…+ λ_pХ_p;

;

.

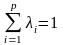Так как Z(Х) – линейная функция, то

Z(Х₀)=Z(λ₁Х₁ + λ₂Х₂+…+ λ_pХ_p)= λ₁Z(Х₁) + λ₂Z(Х₂)+…+ λ_pZ(Х_p).

В этом разложении среди значений Z(Х_i) (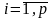 )) выберем наибольшее (пусть оно соответствует угловой точке Х_k (1≤k≤p) и обозначим его через m, т.е. Z(Х_k) = m. Заменим в

Z(Х₀)=Z(λ₁Х₁ + λ₂Х₂+…+ λ_pХ_p)= λ₁Z(Х₁) + λ₂Z(Х₂)+…+ λ_pZ(Х_p)

Каждое значение Z(Х_i) этим наибольшим значением. Тогда так как

;

то

_Z(X₀) ≤ λ₁m + λ₂m+…+ λ_pm = m

Таким образом, Z(X₀) ≤ m = Z(X_k).

По предположению, X₀ – оптимальный план, поэтому, с одной стороны, Z(X₀) ≥ m, а с другой – доказано, что Z(X₀) ≤ m. Значит, Z(X₀) = m = Z(X_k), где X_{k –} угловая точка. Итак, существует угловая точка X_k, в которой линейная функция принимает максимальное значение.

Для доказательства второй части теоремы допустим, что Z(Х) принимает максимальное значение более чем в одной угловой точке, например в точках Х₁,Х₂,…,Х_q ; 1˂q≤p . Тогда Z(X₁) = Z(X₂) =…= Z(X_q) = Z(X₀) = Z_max = m. Если Х – выпуклая линейная комбинация этих угловых точек, т.е.

Х = λ₁Х₁ + λ₂Х₂+…+ λ_qХ_q;

.

то

Z(Х)=Z(λ₁Х₁ + λ₂Х₂+…+ λ_qХ_q)= λ₁Z(Х₁) + λ₂Z(Х₂)+…+ λ_qZ(Х_q)= =λ₁m + λ₂m+…+ λ_qm = m

т.е. линейная функция Z принимает максимальное значение в произвольной точкеХ, являющейся выпуклой линейной комбинацией угловых точек Х₁,Х₂,…,Х_q.

ЗАМЕЧАНИЕ. Если многогранник решений является неограниченной областью, то не каждую точку области можно представить выпуклой линейной комбинацией угловых точек области. В этом случае ЗЛП с многогранником решений, представляющим собой неограниченную область, можно привести к задаче с ограниченной областью, вводя в систему дополнительное ограничение х₁ +х₂+…+х_n≤Q, где Q- достаточно большое число. Введение этого ограничения равносильно отсечению гиперплоскостью х₁ +х₂+…+х_n= Q от многогранной неограниченной области многогранника, для точек которого теорема 2 уже выполняется.

Очевидно, что координаты угловых точек E и F, появившихся в результате введения нового ограничения, зависят от Q. Если в одной из них линейная функция принимает максимальное значение, то, изменяя Q, ее значение можно сделать сколь угодно большим, т.е. целевая функция не ограничена на многограннике решений.