10. Статистичні розподіли. Закон Максвелла про розподіл молекул за швидкостями теплового руху

Незважаючи на повну хаотичність молекулярних рухів, розподіл молекул за швидкостями виявляється не випадковим, а цілком визначеним. Дж. Максвелл, застосовуючи статистичний метод, теоретично розв’язав задачу про розподіл молекул за швидкостями їх поступального руху. У цьому підході будемо вважати, що газ складається з великої кількості N однакових молекул, температура газу однакова у всіх частинах посудини з газом T=const й на газ не діють зовнішні сили F=0.

Якщо розбити діапазон швидкостей на малі інтервали d, то на кожний інтервал швидкості припадатиме деяка кількість молекул dN, швидкість яких лежить в інтервалі від  до +d. Тоді dN/N визначає відносну кількість молекул або ймовірність того, що швидкості молекули знаходяться у цьому інтервалі (;+d). Функція Максвелла, або функція розподілу молекул за швидкостями їх теплового руху, визначає відносну кількість молекул, яка припадає на одиничний інтервал швидкостей: . Застосовуючи методи теорії ймовірності, Максвелл знайшов цю функцію у такому вигляді:

.

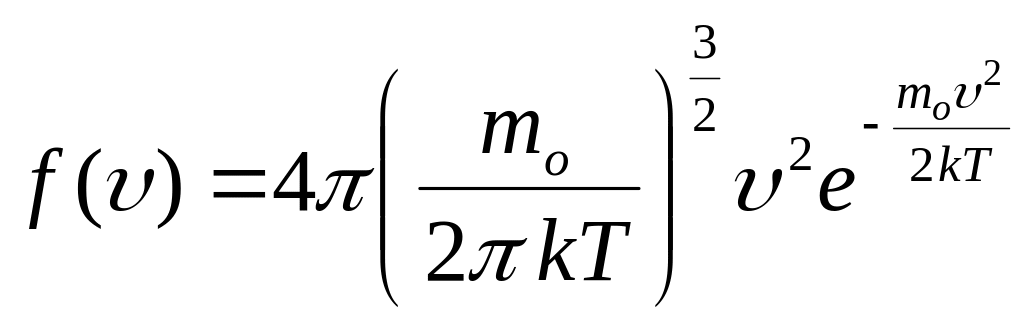К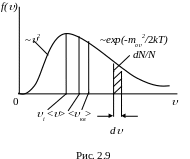 онкретний вигляд функції Максвелла залежить від роду газу (від маси молекули т_о) і від параметра стану (від температури Т). При малих значеннях швидкості f()~², при великих – f()~exp(-m_o²/2kT), тобто прямує до нуля.

Швидкість, за якої f() максимальна, називається найімовірнішою швидкістю _і. Її можна знайти з умови: df/dt = 0. Звідки:

.

За допомогою функції Максвелла визначається також середня арифметична швидкість: ,

і середня квадратична швидкість: .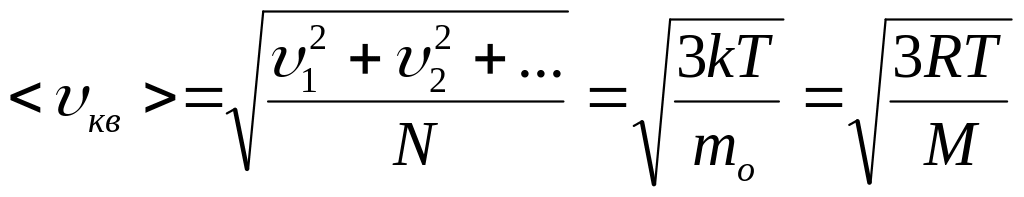

При збільшенні температури максимум кривої f() зміщується у бік більших швидкостей, а його абсолютна величина f_max зменшується (рис. 2.11). Причому площа, яка охоплена кривою f() і віссю Ох, залишається незмінною, оскільки функція розподілу Максвелла повинна задовольняти умову нормування: .

В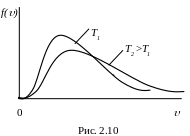 иходячи із функції розподілу молекул за швидкостями f(), можна знайти функцію розподілу молекул за кінетичними енергіями поступального руху f(). Для цього треба від змінної перейти до змінної =т_о²/2. У результаті отримаємо функцію:

.

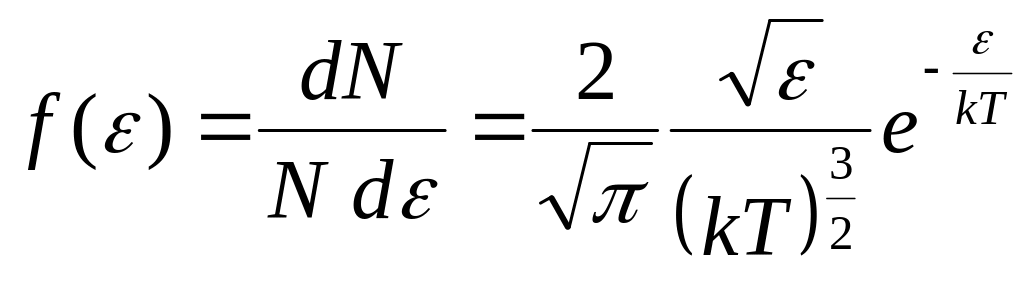Тут dN – кількість молекул, енергія яких знаходиться в інтервалі від  до +d.

11. Барометрична формула. Розподіл Больцмана

Я кщо на молекули не діють зовнішні сили, то вони рівномірно розподіляються по всьому об'єму посудини і для них виконується закон розподілу Максвелла. Розглянемо тепер молекули газу, що знаходиться у полі тяжіння Землі. Якби не було тяжіння, то атмосферне повітря розсіялося б у Всесвіті внаслідок теплового руху молекул. Якби не було теплового руху, то молекули впали б на Землю. Тобто тяжіння і тепловий рух приводять до деякого стаціонарного стану газу, при якому його тиск і концентрація зменшуються з висотою.

Будемо розглядати ідеальний газ, який знаходиться в однорідному полі тяжіння і температура якого постійна Т=const, тобто не змінюється з висотою. Якщо тиск газу на висоті h дорівнює Р, то на висоті h+dh він дорівнює P+dP (рис. 2.11), причому при dh>0 dP<0, оскільки тиск з висотою зменшується.

Згідно із законом Паскаля (див. п. 1.7.1), різниця тисків Р i P+dP дорівнює гідростатичному тиску стовпа газу висотою dh, тобто:

Р – (P+dP) = gdh,

де  – густина газу на висоті h.

Використавши рівняння Менделєєва–Клапейрона, PV = mRT/M, виразимо густину =m/V=PM/RT, звідки:

dР = – , або

.

Уважаючи Т=const й інтегруючи за тиском від P_o до P, а за висотою від 0 до h, отримуємо:

, ,

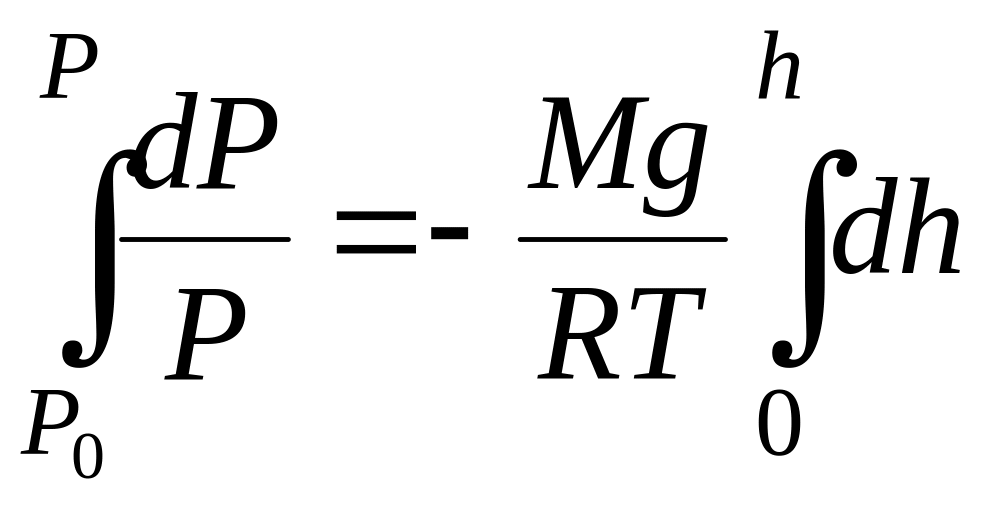звідси

.

Цей вираз називається барометричною формулою, а формула для визначення висоти за зміною тиску

н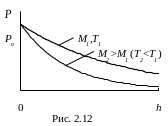 азивається альтиметричною формулою.

З цих формул можна зробити висновок, що тиск газу зменшується із висотою експоненціально (рис. 2.12) і тим швидше, чим більша молярна маса М газу і чим нижча температура Т.

Барометрична формула дає можливість також визначити залежність концентрації газу від висоти. З рівняння стану ідеального газу у вигляді P=nkT при Т=const отримуємо

,

де n_o – концентрація молекул на висоті h = 0.

Оскільки M = m_oN_A, R = k m_oN_A, то

,

де W_n = m_ogh – потенціальна енергія молекули у полі тяжіння.

Із збільшенням висоти концентрація молекул зменшується за експоненціальним законом. При зменшенні температури Т0 концентрація n0, тобто всі молекули опускаються на дно посудини.

Больцман довів, що це співвідношення вірне не тільки для поля тяжіння, але і для інших потенціальних полів, якщо маси молекул однакові і вони знаходяться у стані теплового хаотичного руху. Тому цей вираз

називається розподілом Больцмана для частинок у зовнішньому потенціальному полі.