2.2.Перестановки с повторениями.

Пусть имеется множество, состоящее из n элементов, причем среди них n₁ элементов 1-го типа; n₂ элементов 2-го типа и т.д., n_k элементов k-гo типа, причем n_l+n₂+...+n_k =n. Число перестановок с повторениями из n элементов обозначают и вычисляют по формуле .

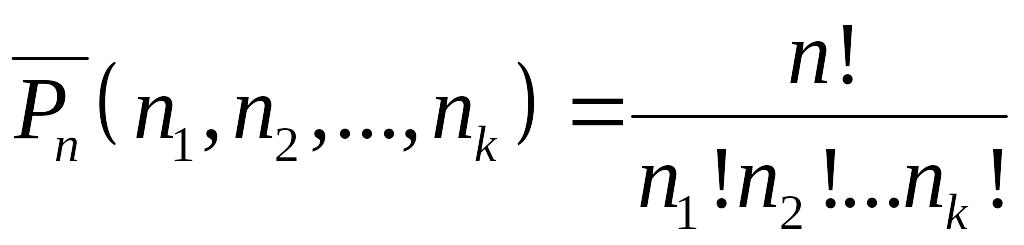Её можно получить так: если бы все n элементов были различными, число перестановок из них равнялось бы n! Чтобы исключить из них перестановки, полученные перестановками одинаковых элементов, разделим на произведение

Пример. Сколько различных слов можно получить, переставляя буквы слова МАТЕМАТИКА? (Ясно, что если бы все буквы были бы различны, то таких слов было бы 10!. Но буква А повторяется 3 раза, а буквы М и Т по 2 раза. Таким образом, всего можно получить слов.)

2.3. Упорядоченные множества. Размещения без повторений.

Будем понимать под кортежем любую последовательность конечного числа элементов. Образование кортежей можно наглядно представить себе следующим образом. Поместим элементы множества Х в мешок и будем извлекать их из него один за другим, записывать извлеченный элемент и класть обратно в мешок. После того как мы сделаем n извлечений, получим один из кортежей длины n, состоящих из элементов множества Х, или размещение с повторениями. Предположим теперь, что мы не возвращаем извлеченные элементы обратно в мешок. Тогда в полученном кортеже не будет повторяющихся элементов. Он будет состоять из n различных элементов, расположенных в определённом порядке. Такие кортежи называют упорядоченными. Одно и то же множество можно упорядочить разными способами (например, множество школьников в классе можно упорядочить по возрасту, по алфавиту, росту, по весу, и так далее).

Число способов, которыми можно упорядочить такие кортеж и называют размещениями без повторений. Формализуем задачу: пусть имеется множество, содержащее n различных элементов. Каждое его упорядоченное подмножество, содержащее m элементов, называют размещением из n элементов по к без повторений. Число размещений из n элементов по k обозначают (от французского слова arrangement, что и означает размещение) и вычисляют по формуле или . Выражение читается, как квадратная энка. В самом деле: первый элемент в размещении из n элементов по k можно выбрать n способами, второй (после выбора первого) можно выбрать (n-1) способами, третий – (n-2) способами и т. д., - k й – (n- k +1) способами. Варьируя способы выбора 1-го элемента со способами выбора 2-го, со способами выбора 3-го элемента и т. д. и, наконец, со способами выбора – k-того элемента, получим n(n - l) ... (n- k+ 1) способов. Таким образом, размещение из n элементов по n без повторений и есть перестановка.

2.4. Размещения с повторениями.

Размещениями из n элементов по k называют упорядоченные k-элементные множества, составленные из различных элементов, причём элементы в множествах могут повторяться. Число размещений с повторениями из n по k обозначается и вычисляется по формуле . В самом деле: 1-й элемент можно выбрать n способами, 2-й элемент – также n способами и т. д., k-й элемент можно выбрать также n способами. Тогда, в соответствии с принципом произведения, сразу получаем этот результат.