9.4. Осмос

При разделении двух растворов различной концентрации или раствора и чистого растворителя полупроницаемой перегородкой (мембраной) возникает поток растворителя от меньшей концентрации к большей, выравнивающий концентрацию. Этот процесс называется осмосом.

О смос характерен не только для истинных, но и для коллоидных растворов. Схема осмоса приведена на рис. 9.4. В сосуд, имеющий полупроницаемую перегородку 3, помещен истинный или коллоидный раствор 1. Полупроницаемая перегородка способна пропускать дисперсионную среду или растворитель, но является препятствием для коллоидных частиц или растворенных веществ. С наружной стороны перегородки находится чистая жидкость (растворитель) 2. Концентрация раствора по обе стороны полупроницаемой перегородки будет различной. Внутри сосуда 1 часть раствора занимают молекулы растворенного вещества или частицы дисперсной фазы, поэтому концентрация жидкости (растворителя или дисперсионная среда) там будет меньше, чем в емкости 2 с чистой жидкостью.

З

Рис. 9.4. Схема осмоса:

1 — сосуд с истинным или коллоидным раствором; 2 — емкость с чистой жидкостью (растворителем); 3 — полупроницаемая перегородка (мембрана)

а счет диффузии жидкость из области более высокой концентрации будет самопроизвольно перемещаться в область меньшей концентрации, т.е. из емкости 2 в емкость 1. Это перемещение на рис. 9.4 показано стрелками. Оно обусловлено тем, что число ударов молекул на мембрану растворителя со стороны чистого или более разбавленного раствора больше, чем со стороны раствора. Это избыточное число ударов и является причиной перемещения растворителя через поры мембраны туда, где его меньше, т.е. в область истинного или коллоидного раствора. Подобное объяснение переноса жидкости является кинетической трактовкой причины осмоса.

Существует еще и термодинамическое объяснение осмотического переноса. Химический потенциал чистой жидкости m₂ превышает химический потенциал этой же жидкости в растворе μ₁. Процесс идет самопроизвольно в сторону меньшего химического потенциала до тех пор, пока не произойдет выравнивание химических потенциалов, т.е. до достижения условия μ₂ = μ₂.

В результате перемещения жидкости в емкости 1 создается избыточное давление p, называемое осмотическим. Растворитель, проникающий в область раствора 1, поднимает уровень жидкости на высоту Н, что компенсирует давление чистого растворителя в сторону раствора. Наступает момент, когда вес столба жидкости в области раствора уравнивается давлением растворителя. Дальнейшего изменения уровня уже не произойдет, а вес столба жидкости над уровнем растворителя будет служить мерой осмотического давления.

Осмотическое давление возникает при движении чистого растворителя в сторону раствора или от более разбавленного раствора в сторону более концентрированного, а следовательно, связано с разностью концентраций растворенного вещества и растворителя. Осмотическое давление — это такое избыточное давление над раствором, которое необходимо для исключения переноса растворителя через мембрану.

Осмотическое давление равно тому давлению, которое производила бы дисперсная фаза (растворенное вещество), если бы она в виде газа при той же температуре занимала тот же объем, что и коллоидная система (раствор). Осмотическое давление не есть проявление какого-либо внешнего воздействия. Оно возникает самопроизвольно, как следствие молекулярно-кинетических свойств дисперсионной среды.

Высота подъема жидкости Н над первоначальным положением раствора количественно определяет осмотическое давление, которое обычно обозначают через π.

Для чистого растворителя и идеального раствора неэлектролитов осмотическое давление выразится формулой

πV = RT In(1–x), (9.8, а)

где V — молярный объем растворителя; х — молярная доля растворенного вещества.

В случае разбавленных растворов неэлектролитов, когда x << 1, можно записать следующее уравнение:

πV = nRT. (9.9)

Согласно определению осмотическое давление можно найти из уравнения состояния (9.9), где n — число молей растворенного вещества.

Если масса растворенного вещества равна q, а молекулярная его масса М, то n = q/М; тогда согласно уравнению (9.9) осмотическое давление равно

(9.10)

Величина q/V есть массовая концентрация растворенного вещества, поэтому осмотическое давление можно определить при помощи следующей формулы

π = (v_м / M)RT. (9.11)

Формула (9.11) является основной для определения осмотического давления. Она позволяет найти зависимость осмотического давления от размеров частиц растворенного вещества. Для этой цели массу дисперсной фазы можно представить в виде

M = mN_A, m = (4 / 3)πr³ρ, (9.12)

где m, r — молекулярная масса и радиус частиц дисперсной фазы; ρ — плотность материала частиц.

Подставив в уравнение (9.11) значение М из формулы (9.12), получим

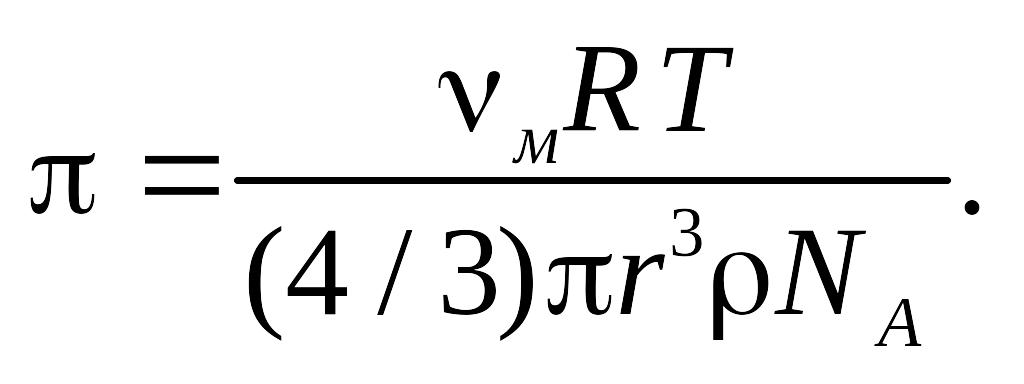(9.13)

Формулу (9.13) используют для определения осмотического давления коллоидных растворов.

Осмотическое давление коллоидных растворов (высокодисперсных систем с жидкой дисперсионной средой) незначительно и составляет всего 1 мм водяного столба или даже меньше (1 мм водяного столба равен примерно 10 Па). Размеры и концентрация частиц в результате агрегации и других процессов могут изменяться. В связи с этим осмотическое давление для высокодисперсных систем непостоянно.

Из формулы (9.13) следует, что осмотическое давление прямо пропорционально концентрации дисперсной фазы и обратно пропорционально размеру частиц этой фазы в третьей степени. Чем меньше размер частиц, тем значительнее осмотическое давление. Если, например, для коллоидных растворов диаметр частиц составляет 100 нм, а размер молекул растворенного вещества — 1 нм, то осмотическое давление молекулярных растворов по сравнению с коллоидными будет в 10⁶ раз больше. Осмотическое давление истинных растворов значительно превышает осмотическое давление коллоидных растворов и составляет для сока сахарной свеклы 35∙10⁵ Па, экстракта кофе — 25∙10⁵ Па, фруктовых соков — 1,5∙10⁵ Па, 6%-го раствора сахара — 60∙10⁵ Па.

Таким образом, осмос, как и все молекулярно-кинетические свойства, характерен для высокодисперсных систем, размеры частиц дисперсной фазы которых не превышают 0,1 мкм.

Упражнения

1. Определить средний сдвиг капель эмульсии радиусом 10 нм за время τ = 4 с при 293 К и вязкости η = 10^–3 Па∙с.

Воспользуемся формулой (9.3):

2. Мыло образует в воде мицеллы, радиус которых равен 12,5 нм. Определите коэффициент диффузии мицелл при 313 К, если вязкость раствора равна 6,5∙ 10^–4 Па∙с.

По формуле (9.7) находим

3. Определить размеры частиц яичного альбумина, находящихся в воде при 293 К, если коэффициент диффузии D = 7,8∙10^–11 м²/с, а вязкость воды равна 10^–3 Па∙ с.

По формуле (9.8) находим

4. Во сколько раз осмотическое давление раствора сока сахарной свеклы π₁ молекулы которого имеют диаметр d₁ = 0,8 нм, превышает осмотическое давление коллоидного раствора свекловичного сока π₂, с диаметром частиц d₂ = 80 нм? Концентрацию коллоидного и молекулярного растворов и их плотности считать одними и теми же.

Согласно формуле (9.13)

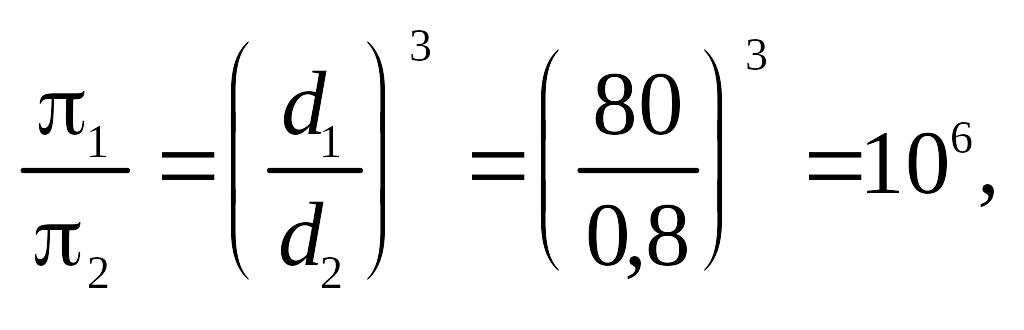
т.е. осмотическое давление молекулярного раствора в 10⁶ раз больше осмотического давления коллоидного раствора.

5. Определить осмотическое давление пыли при 293 К, если ее концентрация 1,5∙10^–2 кг/м², средний радиус частиц 40 мкм, плотность 1,3∙ 10³ кг/м³.

На основании формулы (9.13) находим

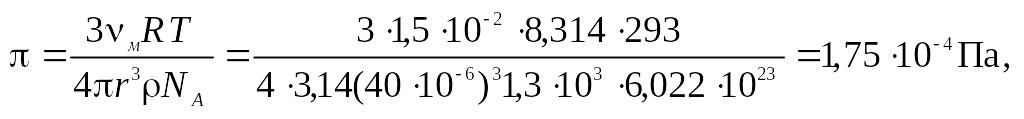
т.е. осмотическое давление незначительно.

Г л а в а 10