9.3. Диффузия

Диффузией называют самопроизвольное распространение вещества из области с большей концентрацией в область с меньшей концентрацией. Различают следующие виды диффузии: молекулярную, ионную и коллоидных частиц.

Диффузия высокодисперсных коллоидных частиц схематически показана на рис. 9.3. В нижней части концентрация частиц больше, чем в верхней, т.е. v₁ > v₂^*. Диффузия идет из области с большей концентрации в область с меньшей, т.е. снизу вверх; направление диффузии на рис. 9.3 показано стрелкой. Диффузия характеризуется определенной скоростью перемещения вещества через поперечное сечение В, которая равна dm/dτ.

На расстоянии Δх разность концентраций составит v₂ – v₁, так как v₂ < v₁, то эта величина отрицательна. Изменение концентрации, отнесенное к единице расстояния, называют градиентом концентрации. Градиент концентрации равен (v₂ – v₁)/Δx, или в д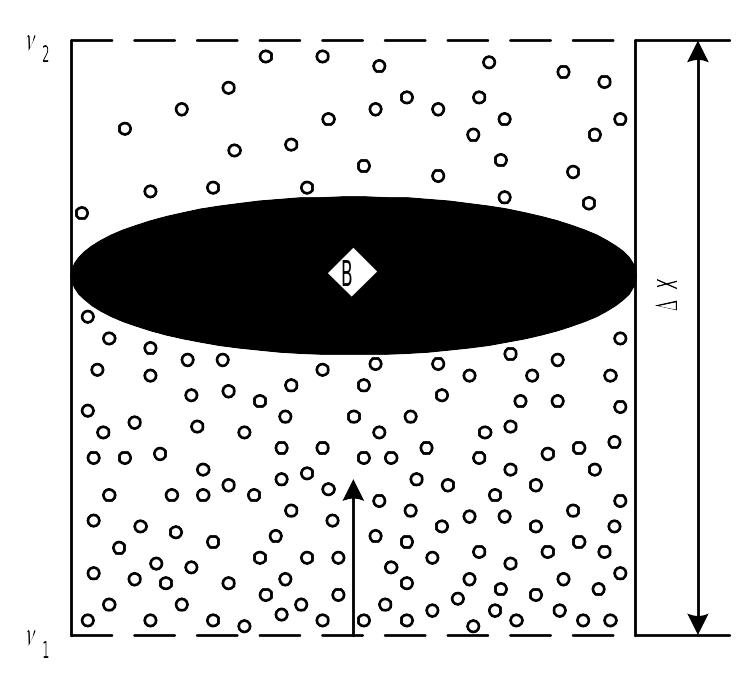 ифференциальной форме, dv/dx.

Скорость перемещения вещества пропорциональна градиенту концентрации и площади В, через которую происходит движение диффузионного потока, т.е.

(9.4)

Скорость диффузии (dm/dt) величина положительная, а градиент концентрации (dv/dx) — отрицателен; по этой причине перед правой частью уравнения (9.4) ставится знак минус.

К

Рис. 9.3. Диффузия частиц в дисперсной системе

оэффициент пропорциональности D называют коэффициентом диффузии. Уравнение (9.4) является основным уравнением диффузии в дифференциальной форме. Оно справедливо для всех видов диффузии, в том числе и для диффузии коллоидных частиц. Основное уравнение диффузии в интегральной форме применимо для двух процессов — стационарного и нестационарного.

Для стационарного процесса градиент концентрации постоянен, т.е. dv/dx = const. Значительное число диффузионных процессов близко к стационарным. Интегрируя уравнение (9.4), получим

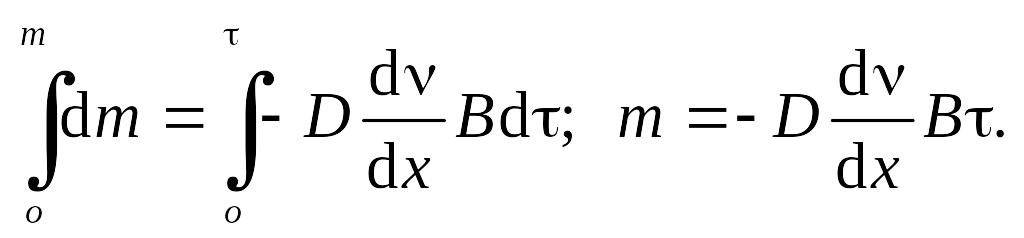(9.5)

Формула (9.5) характеризует первый закон диффузии Фика. Из этой формулы нетрудно определить физический смысл коэффициента диффузии. Если –dv/dх = 1, В = 1 и τ = 1, то m = D, т.е. коэффициент диффузии численно равен массе диффундирующего вещества, когда градиент концентрации, площадь сечения диффузионного потока и время равны единице. Следует говорить лишь о численном равенстве, так как размерность коэффициента диффузии [м²/с] не соответствует размерности массы.

В случае нестационарного процесса градиент концентрации не является постоянной величиной, т.е. dv/dx ≠ const. Интегрирование уравнения (9.4) усложняется, а форма расчетного уравнения учитывает изменение градиента концентрации.

Значения коэффициента диффузии для различных ее видов приведены ниже:

Вид диффузии	Ионная	Молекулярная	Коллоидных частиц
Коэффициент диффузии, м2/с	10–8	10-9	10–10

Коллоидные частицы характеризуются минимальным коэффициентом диффузии. Это означает, что диффузия коллоидных частиц более затруднена по сравнению с молекулярной и ионной. Так, например, скорость диффузии частиц карамели, дисперсной фазой которой является коллоидный раствор, в 100—1000 раз меньше скорости диффузии молекул сахара, формирующих молекулярный раствор. В газах коэффициент диффузии увеличивается до 10^–4, а в твердых телах снижается до 10^–12 м²/с.

Количественно диффузия определяется коэффициентом диффузии, который связан со средним сдвигом, следующим соотношением:

(9.6)

Диффузия высокодисперсных частиц совершается беспорядочно с большей вероятностью в сторону меньшей концентрации. Время, определяемое соотношением (9.6), характеризует продолжительность диффузии. Чем меньше коэффициент диффузии, тем продолжительнее процесс диффузии.

При выводе уравнения (9.6) были приняты следующие допущения: частицы дисперсных систем движутся независимо друг от друга и между ними отсутствует взаимодействие; средняя энергия поступательных движений частиц равна 0,5 kT.

Используя формулу (9.3) для определения среднего сдвига, коэффициент диффузии можно представить в виде

(9.7)

где k — константа Больцмана, равная R/N_A.

Если коэффициент диффузии известен, то по формуле (9.7) можно определить размер частиц:

(9.8)

Как следует из формулы (9.7), чем больше размер частиц, тем меньше коэффициент диффузии и менее интенсивна сама диффузия.

Формулы (9.6)—(9.8) позволили экспериментальным путем определить константу Больцмана и число Авогадро.

В воздухе коэффициент диффузии частиц радиусом 1 нм составляет 1,28 ∙ 10^–6 м²/с. Для частиц радиусом 100 нм коэффициент диффузии снижается до 2,21 ∙ 10^–10 м²/с, для частиц радиусом 10 мкм — до 1,38 ∙10^–10 м²/с. Для частиц, размер которых превышает 10 мкм, т.е. для грубодисперсных систем, коэффициент диффузии и сама диффузия ничтожны.

Диффузия в полной мере проявляется у высокодисперсных систем, ослаблена у среднедисперсных и практически отсутствует у грубодисперсных систем.

Коэффициент диффузии зависит и от формы частиц, что не учитывается в уравнении (9.7). Поэтому при помощи формулы (9.8) можно определить размер только коллоидных шарообразных частиц или приведенный к шарообразному размеру частиц неправильной формы.

Таким образом, диффузия непосредственно связана с броуновским движением; эта связь количественно выражается при помощи уравнений (9.6)—(9.8).