Молекулярно-кинетические свойства высокодисперсных систем

В 1914 г. немецкий физико-химик Вольфганг Оствальд^ обратил внимание широкой научной общественности на мир, как он назвал его, «обойденных величин», т.е. таких дисперсных систем, частицы которых больше размеров молекул, но невидимы в микроскоп. Для подобных систем характерны особые молекулярно-кинетические свойства.

Разработка молекулярно-кинетической теории связана с именем А. Эйнштейна и в начале XX века имела принципиальное значение как прямое доказательство молекулярной природы вещества.

Молекулярно-кинетические свойства обусловлены самопроизвольным движением молекул и проявляются в броуновском движении, диффузии, осмосе и седиментационном равновесии.

9.1. Причина молекулярно-кинетических свойств

Все молекулярно-кинетические свойства вызваны хаотическим тепловым движением молекул дисперсионной среды, которое складывается из поступательного, вращательного и колебательного движений молекул.

Молекулы жидкой и газообразной дисперсионной среды находятся в постоянном движении и сталкиваются друг с другом. Среднее расстояние, которое проходит молекула до столкновения с соседней, называют средней длиной свободного пробега. Для молекул воздуха при 298 К она составляет 71 нм, а при 293 К — 20 нм. Из приведенных данных следует, что длина свободного пробега значительно превышает размеры самих молекул.

Молекулы обладают различной кинетической энергией. Тем не менее при данной температуре среднее значение кинетической энергии молекул остается всегда постоянным для одной молекулы и одного моля оно составляет

(9.1)

где m, М — масса одной молекулы и одного моля; v — скорость движения молекул; k  — константа Больцмана; R — универсальная газовая постоянная.

Флуктуация значений кинетической энергии молекул дисперсионной среды (т.е. отклонение от среднего) и является причиной молекулярно-кинетических свойств.

Установление и изучение молекулярно-кинетических свойств стало возможным в результате применения статистических методов исследования. Эти методы предполагают применение к системам, состоящим из множества элементов (в данном случае молекул), теории вероятности. Исходя из допущений о беспорядочности движения отдельных молекул, теория определяет наиболее вероятное сочетание для систем, состоящих из множества молекул.

Статистические методы, разработанные для изучения молекулярно-кинетических свойств, послужили основой для исследований некоторых важных физических и физико-химических явлений.

Молекулярно-кинетические свойства проявляются в жидкой и газообразной дисперсионной среде, молекулы которых обладают определенной подвижностью.

9.2. Броуновское движение

Броуновским называют непрерывное, хаотическое, равновероятное для всех направлений движение мелких частиц, взвешенных в жидкости или газах, за счет воздействия молекул дисперсионной среды.

Аэрозольную частицу диаметром 100 нм окружают примерно 10⁵ газовых молекул, частота колебаний которых (применительно к двухатомным молекулам) составляет 10¹⁴ с^-1. Следовательно, одна аэрозольная частица за счет газовых молекул может испытать 10¹⁹ ударов за 1 с. Если бы сила ударов, которые получает частица со всех сторон, была одинакова, то частица «топталась» бы на месте.

Мельчайшие частицы незначительной массы испытывают неодинаковые удары со стороны молекул дисперсионной среды; результирующая сила F, которая заставляет частицы двигаться, показана на рис. 9.1 жирной стрелкой. Направление и импульс этой силы непрерывно меняются, поэтому частицы совершают хаотическое движение.

Молекулы дисперсионной среды таким же образом действуют на частицы средне- и грубодисперсных систем. В связи со значительным размером частиц этих систем число ударов молекул резко увеличивается. По законам статистики подобное обстоятельство означает, что импульс действия сил со стороны молекул среды взаимно компенсируется, а значительная масса и инерция относительно крупных частиц способствует тому, что воздействие молекул остается без последствий. Поэтому броуновское движение наиболее интенсивно проявляется в отношении высокодисперсных систем.

Направление результирующей силы F (см. рис. 9.1), вызванной ударами молекул, и движение самих молекул все время изменяются. Определить эти изменения и связать их с молекулярно-кинетическими свойствами среды удалось в 1907 г. независимо друг от друга А. Эйнштейну и М. Смолуховскому.

Рис. 9.1. Воздействие молекул дисперсионной среды на частицу 1 дисперсной фазы.

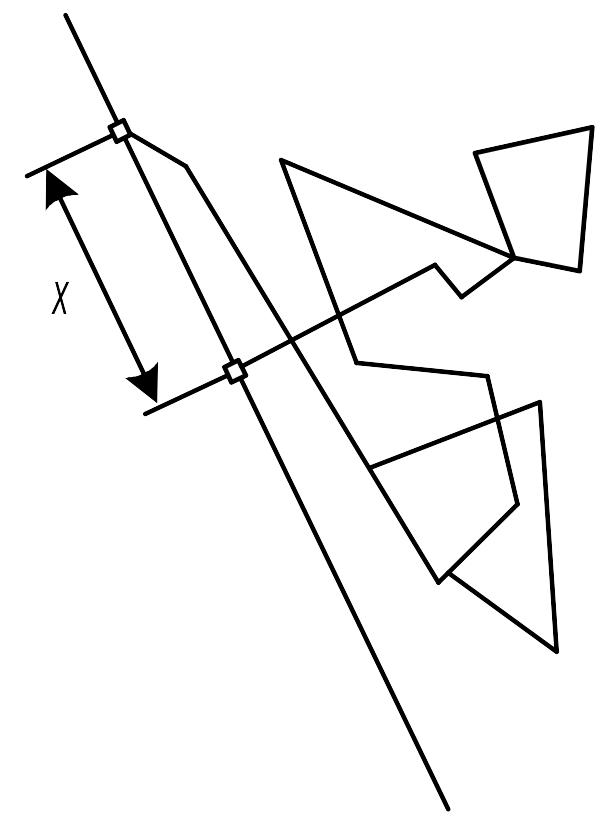
Рис. 9.2. Сдвиг частиц.

В основу их расчетов был взят не истинный путь частиц дисперсной фазы, а сдвиг частиц (рис. 9.2). Если путь частицы определяется ломаной линией, то сдвиг х характеризует изменение координат частицы за определенный отрезок времени. Средний сдвиг будет определять среднеквадратическое смещение частицы, которое определяется по уравнению

, (9.2)

где х₁, х₂, x_i — сдвиг частиц за определенное время.

Теория броуновского движения исходит из представления о взаимодействии случайной силы f(τ), которая характеризует удары молекул, силы F_τ, зависящей от времени, и силы трения при движении частиц дисперсной фазы в дисперсионной среде со скоростью n. Уравнение случайного броуновского движения (уравнение Ланжевена) имеет следующий вид:

m(dν/dt) + ην = F_τ + f(τ), (9.2, а)

где m — масса частицы; η — коэффициент вязкости дисперсионной среды.

Для больших промежутков времени (τ >> m/η) инерцией частиц, т.е. членом m(dν/dτ), можно пренебречь. После интегрирования уравнения (9.2, а) при условии, что среднее произведение импульсов случайной силы равно нулю, находят среднее значение флуктуации (средний сдвиг):

(9.3)

где τ — время; r — радиус частиц дисперсной фазы; N_A — число Авогадро.

В формуле (9.3) отражены параметры дисперсной фазы и дисперсионной среды: величина RT/N_A характеризует молекулярно-кинетические свойства дисперсионной среды, а η — ее вязкость; радиус частиц r — это параметр, относящийся к дисперсной фазе, а время t определяет взаимодействие дисперсионной среды с дисперсной фазой. Формула (9.3) подтверждена экспериментально.

Кроме поступательного возможно вращательное броуновское движение, характерное для двухмерных частиц и частиц неправильной формы (нитей, волокон, хлопьев и др.).

Средний сдвиг частиц различного размера за одну секунду в воздушной среде характеризуется значениями:

Радиус частиц, мкм 10^-3 0,1 10

Максимальные значения среднего сдвига, мкм 1,28 ∙ 10³ 0,168 0,0123

Средний сдвиг для частиц высокодисперсных систем размером 10^–3 — 10^–1 мкм (или 1—100 нм) может достигать нескольких миллиметров.

Броуновское движение наиболее ярко выражено у высокодисперсных систем, а его интенсивность зависит от дисперсности (см. рис. 1.2). Для среднедисперсных систем средний сдвиг составляет единицы или доли микрометров. Если размер частиц превышает 10 мкм, то броуновским движением можно пренебречь. Это обстоятельство является одним из факторов, ограничивающим верхний размер среднедисперсных систем значением 10 мкм.