
2.1. Расчет цепей первого порядка.
Рассмотрим цепь на рис.2.1.

Рис.2.1
Описывающее уравнение набираем на рабочем поле:
![]()
Там же ниже записываем начальные условия:

Используем значок
![]() из (Ealuetion Toolbar)
из (Ealuetion Toolbar)
слева вводим решаемое ДУ, причем без “=”, правую часть переносим налево с отрицательным знаком, далее используем оператор Лапласа (laplace) из меню Символы (Simbol), через запятую – переменную по которой будет проводиться интегрирование. На экране увидим:

Далее следует упростить полученное выражение. Для этого переменную laplace(i(t),t,s), которая соответствует корню ОДУ, заменим, например на Z, которая легче воспринимается визуально. Напишем:
![]()
Проводить дальнейшие преобразования также невозможно, из-за присутствия элемента i(0), поэтому мы заменим его на i0, т.к. это простая константа, задающая начальные условия для решения задачи Коши.
После того как дифференциальное уравнение (ДУ) приведено к приемлемому виду, его необходимо разрешить относительно Z. Для этого воспользуемся оператором символьного решения solve из панели Simbol.
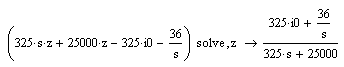
Чтобы привести решение ДУ, к полученному решению-изображению необходимо пременить обратное преобразование Лапласа.

Полученный результат и будет являться решением уравнения. Для получения решения задачи Коши, нужно задать начальные условия, а менно i0.
![]()
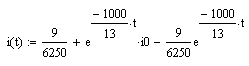
Теперь можно построить график полученного решения Рис. 2.2.:

Рис.2.2.
Именим параметры
цепи в начале рабочего поля, увидим на
экране приведенные н иже
формулы и график (Рис 2.3.):
иже
формулы и график (Рис 2.3.):
Рис.2.3.
Изменим параметры цепи еще раз, увидим результат на рис 2.4.:

Рис.2.4.
Для других параметров рис.2.5:
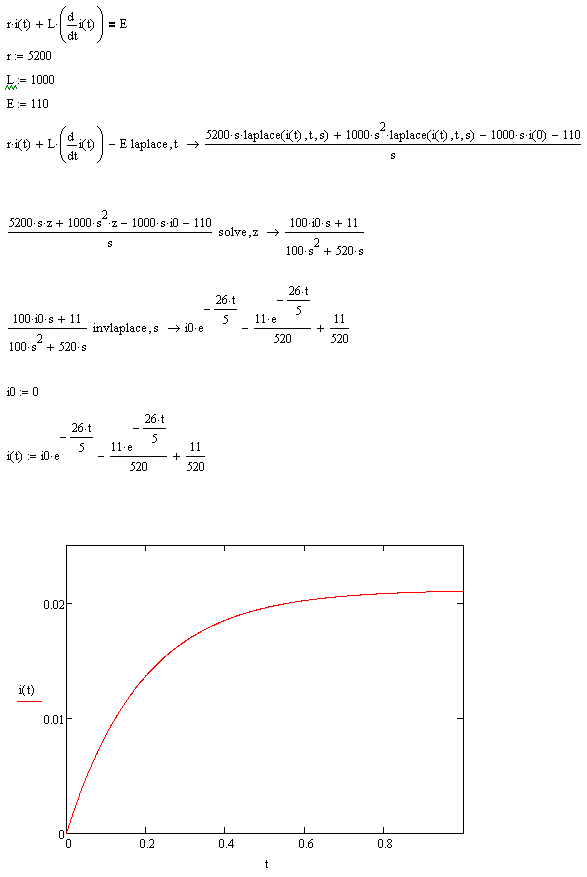
Рис.2.5.
2.2. Расчет цепей второго порядка.
Рассмотим случай, когда катушка и конденсатор соединены последовательно Рис 2.6.
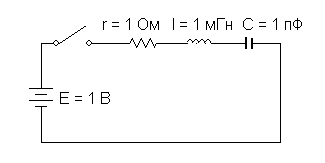
Рис. 2.6.
Запишем на рабочем поле программы уравнение в соответствии со вторым законом Кирхгофа:

До замыкания ключа:

Выразим ток i(t) через напряжение на конденсаторе Uc(t):

Воспользуемся функцией преобразования Лапласа, которая находится на панели ключевой символики, получим на экране формулу как на рис.2.7.

Рис.2.7
Сделаем замену L=laplace(Uc(t),t,s), C1=U(0) (начальные условия для конденсатора), C2= dUc(t)/dt, t=0 (начальные условия для катушки)
Теперь выразим переменную L увидим изображение :

Зададим начальные условия: С1=0, С2 = 0, U0 = 0
Применим функцию обратного преобразования Лапласа :

Ток находим по формуле находим ток в цепи:
![]()
Рассмотрим случай когда катушка и конденсатор соединены параллельно:

Рис.2.8
Запишем на рабочем поле параметры цепи:
![]()
Запишем уравнение по второму и первому законам Кирхгофа для данной цепи ниже строки с параметрами:

Найдем ток i1(t). Для этого выразим напряжение на конденсаторе Uc(t) через ток i1(t). Сделаем эту запись еще ниже:
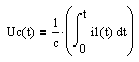
Уравнение примет вид:
![]()
Воспользуемся функцией преобразования Лапласа:

Сделаем замену L1 = laplace(Uc(t),t,s), C1=Uc(0)=0
Выразим переменную L1

Применим функцию обратного преобразования Лапласа и найдем Uc(t):

Найдем ток i1(t):

Теперь найдем ток i2(t), для чего воспользуемся функцией преобразования Лапласа:
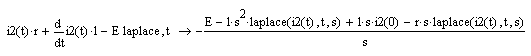
Сделаем замену L2=laplace(i1(t),t,s), C2=i2=0 (начальные условия для катушки). Теперь выразим L2:
![]()
Используя функцию обратного преобразования Лапласа и найдем i2(t):


Тогда ток i(t) будет равен:

![]()
ЗАКЛЮЧЕНИЕ
После знакомства с данным учебным пособием студенты могут начать работать в пакете Mathcad и применять этот мощный инструмент в своей практике. Его использование позволит лишь начать работать в Mathcad, дальнейшее углубление знаний и навыков можно получить при использовании более полной литературы по этому пакету.
Проведенные экспериментальные исследования позволят студентам более грамотно использовать современную компьютерную технику в своей практической деятельности.
СПИСОК ЛИТЕРАТУРЫ
Дьяконов, В.П. Mathcad 11/12/13 в математике: cправочник/В.П.Дьяконов
– М.: Горячая линия – Телеком, 2007. – 958с.
Беглецов, Ю.П. Электрические цепи переменного тока. Руководство по выполнению базовых экспериментов. ЭЦПЕТ.001 РБЭ (902)/ Ю.П.Беглецов Ю.П.Галишников, П.Н. Сенигов П.Н. – Челябинск: ООО «Учебная техника», 2003. – 133 с.
Бессонов, Л.А. Теоретические основы электротехники. Электрические цепи: учебник/Л.А.Бессонов – 10-е изд. – М.: Гардарики, 2000. - 638 с.
