22. Таблица основных интегралов

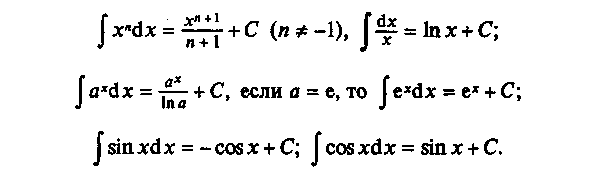
23. О приближенных вычислениях

Числовые значения величин, которыми приходится оперировать при решении физических задач, являются большей частью прибли­женными. Поэтому при вычислениях нужно придерживаться сле­дующих правил:

1. Достаточно проводить вычисления с числами, содержащими не более знаков, чем в исходных данных, так как с помощью вы­числений невозможно получить результат более точный, чем исход­ные данные.

2. При сложении или вычитании чисел, имеющих различную точность, более точное должно быть округлено до точности менее точного. Например: 9,6 + 0,176 = 9,6 + 0,2 = 9,8; 100,8-0,4=100,4.

3. При умножении (делении) следует округлять сомножители так, чтобы каждый из них содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим числом значащих цифр. Напри­мер: 342∙378 = 129∙10³, но не 129276 и не 129300; 0,148∙ 0,183 = 7,65∙10 ^-3, но не 0,0076494; 0,350:3 = 0,117, но не 0,11667.

4. При извлечении корня n-й степени результат должен иметь столько значащих цифр, сколько их имеет подкоренное выражение.

Например:

5. При вычислении сложных выражений следует соблюдать пра­вила в зависимости от вида проводимых действий.

6. Когда число мало отличается от единицы, можно пользовать­ся приближенными формулами.

Если а, b, с — малы по сравнению с единицей (меньше 0,05), то:

1. (1±a)(1±b)(1±с) = 1±a±b±с;

2. ;

3. ;

4) ;

5) ;

6) ;

7) .

7. Если угол , то (в радианах).

Соблюдая эти правила, студент сэкономит время на вычисление искомых величин при решении физических задач.

Литература

1. Дмитриева В.Ф, Прокофьев В.Л. Основы физики. - М.: Высш. шк, 2003.

2. Трофимова Т.И. Курс физики. -М: Высш. шк., 2004.

3. Яворский Б.М., Детлаф А.А. Справочник по физике. -М: Наука, 1996.

4. Детлаф А.А., Яворский Б.М. Курс физики. -М.: Высш. Шк., 2000.

5. Волькенштейн В.С. Сборник задач по общему курсу физики. -М.: Наука, 2000.

6. Трофимова Т. И., Павлова З.Г. Сборник задач по курсу физики с решениями. -М.: Высш. Шк, 2004.

60