Вариант 10
единичные векторы, угол между которыми 45°. Найти скалярное произведение векторов
и
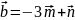.Выразить вектор
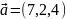в базисе, состоящем из векторов:
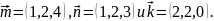
Даны векторы
и
.
Найти
угол между векторами
и
.
Найти длину вектора
.
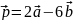Построить уравнение прямой, проходящей через точку пересечения прямых
3y+x-2=0 и 7x-4y+5=0 и перпендикулярной прямой y=-7x+1. Найти расстояние до этой прямой от точки (-1,4).
Найти уравнения и длины медианы, биссектрисы и высоты, опущенных из вершины A в треугольнике ABC, если A=(-1,1), B=(1,9), C=(5,3).
Парабола с вершиной в точке (1,-2) проходит через точку (-1,5) и симметрична относительно оси OX. Найти фокус и уравнение директрисы параболы. Построить ее.
Построить уравнение плоскости, проходящей через точку M (-6,5,-3) параллельно прямым
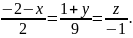Найти
расстояние до этой плоскости от точки
N
(10,1,-2).
Построить уравнение прямой, проходящей через точки
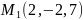и
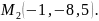Найти
расстояние до этой прямой от точки
Вариант 11
единичные векторы, угол между которыми 60°. Найти скалярное произведение векторов
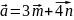и
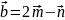.Выразить вектор
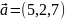в базисе, состоящем из векторов:
Даны векторы
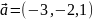и
.
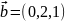Найти
угол между векторами
и
.
Найти длину вектора
.
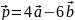Построить уравнение прямой, проходящей через точку пересечения прямых
2y-7x-5=0 и 2x-3y+1=0 и перпендикулярной прямой y=6x+1. Найти расстояние до этой прямой от точки (-1,4).
Найти уравнения и длины медианы, биссектрисы и высоты, опущенных из вершины A в треугольнике ABC, если A=(7,0), B=(5,4), C=(2,1).
Найти полуоси, координаты фокусов и эксцентриситет эллипса
.
Нарисовать его.Построить уравнение плоскости, проходящей через точку M (1,-2,13) перпендикулярно плоскости
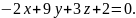Найти расстояние до этой плоскости от
точки N
(-4,11,0).
Построить уравнение прямой, проходящей через точки
и
Найти
расстояние до этой прямой от точки
Вариант 12
единичные векторы, угол между которыми 60°. Найти скалярное произведение векторов
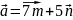и
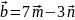.Выразить вектор
в базисе, состоящем из векторов:
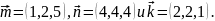
Даны векторы
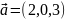и
.
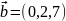Найти
угол между векторами
и
.
Найти длину вектора
.
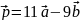Построить уравнение прямой, проходящей через точку пересечения прямых
3y+x-2=0 и x-9y+3=0 и перпендикулярной прямой y=4x-4. Найти расстояние до этой прямой от точки (-1,4).
Найти уравнения и длины медианы, биссектрисы и высоты, опущенных из вершины A в треугольнике ABC, если A=(3,2), B=(3,4), C=(5,12).
Найти координаты вершин, координаты фокусов, уравнения асимптот и эксцентриситет гиперболы
.
Нарисовать ее.Построить уравнение плоскости, проходящей через точку M (-6,-9,2) перпендикулярно прямой
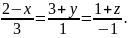Найти расстояние до этой плоскости от
точки N
(-6,1,-3).
Построить уравнение прямой, проходящей через точки
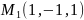и
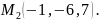Найти
расстояние до этой прямой от точки
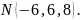
Вариант 13
единичные векторы, угол между которыми 60°. Найти скалярное произведение векторов
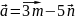и
.Выразить вектор
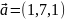в базисе, состоящем из векторов:
Даны векторы
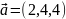и
.
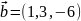Найти угол между векторами и . Найти длину вектора .
Построить уравнение прямой, проходящей через точку пересечения прямых
y+10x-5=0 и x-7y+1=0 и перпендикулярной прямой y=0,5x-1. Найти расстояние до этой прямой от точки (-1,4).
Найти уравнения и длины медианы, биссектрисы и высоты, опущенных из вершины A в треугольнике ABC, если A=(2,10), B=(-1,4), C=(5,1).
Парабола с вершиной в точке (3,-2) проходит через точку (1,4) и симметрична относительно оси OY. Найти фокус и уравнение директрисы параболы. Построить ее.
Построить уравнение плоскости, проходящей через точку M (-1,1,-7) параллельно прямым
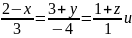
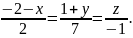Найти
расстояние до этой плоскости от точки
N
(1,1,-5).
Построить уравнение прямой, проходящей через точки
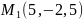и
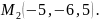Найти
расстояние до этой прямой от точки
