19. Интегрирование некоторых иррациональных функций
1.
Интегралы вида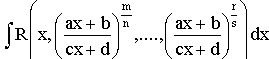 
рационализируются
подстановкой 
,
где 
-
общий знаменатель дробей 
.
2.
Интеграл от дифференциального
бинома 
выражается
через конечную комбинацию элементарных
функций лишь в трех случаях:
2.1.
-
целое число, подстановка 
(
-
наименьший общий знаменатель дробей 
).
2.2.
-
целое число, подстановка 
(
-
знаменатель дроби 
).
2.3.
-
целое число, подстановка 
(
-
знаменатель дроби 
).
В
остальных случаях интеграл от
дифференциального бинома не выражается
через конечное число элементарных
функций.
3.
Интеграл вида 
,
подстановка 
.
4.
Интеграл вида 
,
подстановка 
или 
.
5.
Интеграл вида 
,
подстановка 
или 
.
6.
Интеграл вида 
с
помощью подстановки 
сводится
к одному из интегралов (3) – (5).
7.
Интеграл вида 
можно
также упростить подстановками Эйлера:
7.1. Если 
7.2. Если 
7.3. Если трехчлен 
имеет
различные корни 
,
то 
.
Интегрирование биномиальных дифференциалов
рационализуется лишь в трех случаях:
1) 
подстановка 
где k -
общий знаменатель m и n;
2) 
подстановка 
где k -
знаменатель p;
3) 
подстановка 
где k -
знаменатель p.
20. Интегрирование рационально-тригонометрических функций
всегда
рационализует универсальная подстановка 
Специальные подстановки
1) Если R (-sin x, cos x) = -R (sin x, cos x), то рационализует подстановка cos x = t.
2) Если R (sin x, -cos x) = -R (sin x, cos x), то рационализует подстановка sin x = t.
3) Если R (-sin x, -cos x) = R (sin x, cos x), то рационализует подстановка tg x = t.
Скажем дружно спасибо автору!
Плут Павел.
Гр.: Э-52