
- •2. Первый замечательный предел:
- •3. Точки разрыва
- •Устранимые точки разрыва
- •Точки разрыва первого и второго рода
- •Свойства Локальные
- •Глобальные
- •Связь между дифференцируемостью и непрерывностью функции
- •10. Основные теоремы дифференциального исчисления
- •Точная формулировка
- •13. Необходимые условия существования локальных экстремумов
- •Достаточные условия существования локальных экстремумов
- •16. Определение первообразной.
- •17. Замена переменной в неопределенном интеграле
- •Интегрирование по частям
- •19. Интегрирование некоторых иррациональных функций
- •20. Интегрирование рационально-тригонометрических функций
16. Определение первообразной.
Первообразной
функции f(x) на
промежутке (a;
b) называется
такая функция F(x),
что выполняется равенство ![]() для
любого х из
заданного промежутка.Если принять во
внимание тот факт, что производная от
константы С равна
нулю, то справедливо
для
любого х из
заданного промежутка.Если принять во
внимание тот факт, что производная от
константы С равна
нулю, то справедливо
равенство ![]() .
Таким образом, функция f(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
.
Таким образом, функция f(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение
неопределенного интеграла.Все
множество первообразных функции f(x) называется
неопределенным интегралом этой функции
и обозначается ![]() .
.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
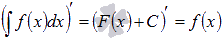 Производная
результата интегрирования равна
подынтегральной функции.
Производная
результата интегрирования равна
подынтегральной функции.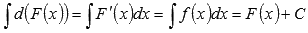 Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.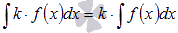 ,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.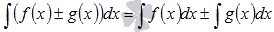 Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
17. Замена переменной в неопределенном интеграле
Замена
переменной в неопределенном интеграле
производится с помощью подстановок
двух видов:
а) ![]() ,
где
,
где ![]() –
монотонная, непрерывно дифференцируемая
функция новой переменной t. Формула
замены переменной в этом случае:
–
монотонная, непрерывно дифференцируемая
функция новой переменной t. Формула
замены переменной в этом случае: ![]() ;
б)
;
б) ![]() ,
где U –
новая переменная. Формула замены
переменной при такой
подстановке:
,
где U –
новая переменная. Формула замены
переменной при такой
подстановке: ![]() .
Примеры.
1. Найти интеграл
.
Примеры.
1. Найти интеграл ![]() .
Решение. Перепишем данный интеграл в
виде
.
Решение. Перепишем данный интеграл в
виде ![]() .
Так как производная выражения
.
Так как производная выражения ![]() равна
2/х,
а второй множитель 1/хотличается
от этой производной только постоянным
коэффициентом 2, то нужно применить
подстановку
равна
2/х,
а второй множитель 1/хотличается
от этой производной только постоянным
коэффициентом 2, то нужно применить
подстановку ![]() .
Тогда
.
Тогда ![]() .
Следовательно,
.
Следовательно,
![]() .
2. Найти интеграл
.
2. Найти интеграл ![]() .
Решение.
.
Решение. ![]() ,
тогда
,
тогда ![]() и
и
![]() .
.
Интегрирование по частям
Нахождение
интеграла ![]() по
формуле
по
формуле ![]() называется
интегрированием по частям.
Здесь U=U(х),υ=υ( x)
непрерывно дифференцируемые функции
от х.
С помощью этой формулы нахождение
интеграла сводится к отысканию другого
интеграла
называется
интегрированием по частям.
Здесь U=U(х),υ=υ( x)
непрерывно дифференцируемые функции
от х.
С помощью этой формулы нахождение
интеграла сводится к отысканию другого
интеграла ![]() ,
ее применение целесообразно в тех
случаях, когда последний интеграл либо
проще исходного, либо ему подобен.
При этом за υ берется такая функция,
которая при дифференцировании упрощается,
а за dU –
та часть подынтегрального выражения,
интеграл от которой известен или может
быть найден.
Так например,
для интегралов вида
,
ее применение целесообразно в тех
случаях, когда последний интеграл либо
проще исходного, либо ему подобен.
При этом за υ берется такая функция,
которая при дифференцировании упрощается,
а за dU –
та часть подынтегрального выражения,
интеграл от которой известен или может
быть найден.
Так например,
для интегралов вида ![]() ,
, ![]() ,
, ![]() ,
где P(x)
– многочлен, за υ следует принять P(x),
а за dU соответствует
выражение
,
где P(x)
– многочлен, за υ следует принять P(x),
а за dU соответствует
выражение ![]() ,
, ![]() .
Для интегралов вида
.
Для интегралов вида ![]() за
υ принимаются соответственно функции
за
υ принимаются соответственно функции ![]() ,
а за
,
а за ![]() –
выражение P(x)dx.
–
выражение P(x)dx.
18.
Для
интегрирования рациональной функции ![]() ,
где P(x) и Q(x) -
полиномы, используется следующая
последовательность шагов:
,
где P(x) и Q(x) -
полиномы, используется следующая
последовательность шагов:
-Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
-Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
-Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
-Вычислить интегралы от простейших дробей.
Шаг 1. Преобразование неправильной рациональной дроби
Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочленP(x) на Q(x). Получим следующее выражение:
![]()
где - правильная рациональная дробь.
Шаг 2. Разложение знаменателя на простейшие дроби
Запишем многочлен знаменателя Q(x) в виде
![]()
где квадратичные функции являются несократимыми, то есть не имеющими действительных корней.
Шаг 3. Разложение рациональной дроби на сумму простейших дробей.
Запишем рациональную функцию в следующем виде:

Общее число неопределенных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , ... должно быть равно степени знаменателя Q(x). Затем умножим обе части полученного уравнения на знаменатель Q(x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , .... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов.
Шаг 4. Интегрирование простейших рациональных дробей.
Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:
![]()
![]()

![]()
![]()
![]()
![]()
Интеграл ![]() может
быть вычислен за k шагов
с помощью формулы редукции
может
быть вычислен за k шагов
с помощью формулы редукции

