
- •2. Первый замечательный предел:
- •3. Точки разрыва
- •Устранимые точки разрыва
- •Точки разрыва первого и второго рода
- •Свойства Локальные
- •Глобальные
- •Связь между дифференцируемостью и непрерывностью функции
- •10. Основные теоремы дифференциального исчисления
- •Точная формулировка
- •13. Необходимые условия существования локальных экстремумов
- •Достаточные условия существования локальных экстремумов
- •16. Определение первообразной.
- •17. Замена переменной в неопределенном интеграле
- •Интегрирование по частям
- •19. Интегрирование некоторых иррациональных функций
- •20. Интегрирование рационально-тригонометрических функций
10. Основные теоремы дифференциального исчисления
Кольцо
непрерывных на ![]() и
гладких на
и
гладких на ![]() функций
обладает рядом важных свойств:
функций
обладает рядом важных свойств:
Теорема Ролля: если
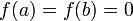 ,
то имеется точка
,
то имеется точка 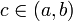 максимума
или минимума, в которой
максимума
или минимума, в которой 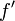 обращается
в нуль.
обращается
в нуль.Теорема Лагранжа: существует такая точка , что
![]()
Теорема Коши: если
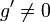 на
,
то существует такая точка
,
что
на
,
то существует такая точка
,
что
![]()
Теорема Ферма. Пусть функция f (х) определена на интервале (а, b) и в некоторой точке х0 (а, b) имеет локальный экстремум. Тогда, если в точке х0 существует конечная производная f '(x0), то f '(x0) = 0.
11.
Правило
Бернулли-Лопита́ля —
метод нахождения пределов
функций, раскрывающий
неопределённости вида ![]() и
и ![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
Точная формулировка
Условия:
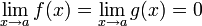 или
или 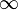 ;
;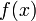 и
и 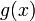 дифференцируемы
в проколотой окрестности
;
дифференцируемы
в проколотой окрестности
;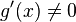 в
проколотой окрестности
;
в
проколотой окрестности
;существует
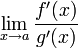 ,
,
тогда
существует ![]() .
.
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
|
|
|
|
|
|
|
Для раскрытия неопределённостей видов , , пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
![]()
![]()
![]()
Для раскрытия неопределённостей типа используется следующий алгоритм:
-Выявление старшей степени переменной;
-Деление на эту переменную как числителя, так и знаменателя.
Для раскрытия неопределённостей типа существует следующий алгоритм:
-Разложение на множители числителя и знаменателя;
-Сокращение дроби.
Для раскрытия неопределённостей типа иногда удобно применить следующее преобразование:
Пусть ![]() и
и ![]()
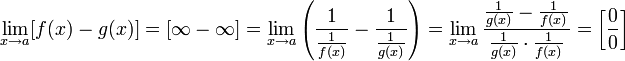
12.
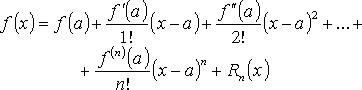 -
Формула Тейлора
-
Формула Тейлора
Важнейшие разложения по формуле Тейлора
![]()
![]()
![]()
![]()
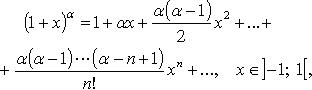
![]()
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
13. Необходимые условия существования локальных экстремумов
Из леммы Ферма вытекает следующее:
Пусть точка является точкой экстремума функции , определенной в некоторой окрестности точки .
Тогда
либо производная ![]() не
существует, либо
не
существует, либо ![]() .
.
Достаточные условия существования локальных экстремумов
Пусть
функция ![]() непрерывна
в
непрерывна
в ![]() и
существуют конечные или бесконечные
односторонние производные
и
существуют конечные или бесконечные
односторонние производные ![]() .
Тогда при условии
.
Тогда при условии
![]()
является точкой строгого локального максимума. А если
![]()
то является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке
Пусть функция непрерывна и дважды дифференцируема в точке . Тогда при условии
и ![]()
является точкой локального максимума. А если
и ![]()
то является точкой локального минимума.
Пусть
функция
дифференцируема ![]() раз
в точке
и
раз
в точке
и ![]() ,
а
,
а ![]() .
.
14.
Дифференцируемая
функция называется выпуклой
вниз на
интервале Х,
если ее график расположен не ниже
касательной к нему в любой точке
интервала Х.
Дифференцируемая
функция называется выпуклой
вверх на
интервале Х,
если ее график расположен не выше
касательной к нему в любой точке
интервала Х.
Выпуклую
вверх функцию часто называют выпуклой,
а выпуклую вниз – вогнутой.
 Точка
Точка ![]() называется точкой
перегиба графика функции y
= f(x),
если в данной точке существует касательная
к графику функции (она может быть
параллельна оси Оу)
и существует такая окрестность точки
называется точкой
перегиба графика функции y
= f(x),
если в данной точке существует касательная
к графику функции (она может быть
параллельна оси Оу)
и существует такая окрестность точки ![]() ,
в пределах которой слева и справа от
точки М график
функции имеет разные направления
выпуклости.
Другими словами,
точка М называется
точкой перегиба графика функции, если
в этой точке существует касательная и
график функции меняет направление
выпуклости, проходя через нее.
Если
необходимо, обратитесь к разделу касательная
к графику функции в точке,
чтобы вспомнить условия существования
невертикальной и вертикальной
касательной.
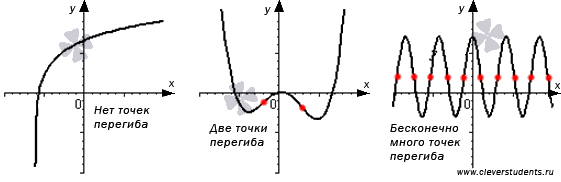
На рисунке ниже
представлены несколько примеров точек
перегиба (отмечены красными точками).
Заметим, что некоторые функции могут
не иметь точек перегиба, а другие могут
иметь одну, несколько или бесконечно
много точек перегиба.
,
в пределах которой слева и справа от
точки М график
функции имеет разные направления
выпуклости.
Другими словами,
точка М называется
точкой перегиба графика функции, если
в этой точке существует касательная и
график функции меняет направление
выпуклости, проходя через нее.
Если
необходимо, обратитесь к разделу касательная
к графику функции в точке,
чтобы вспомнить условия существования
невертикальной и вертикальной
касательной.
На рисунке ниже
представлены несколько примеров точек
перегиба (отмечены красными точками).
Заметим, что некоторые функции могут
не иметь точек перегиба, а другие могут
иметь одну, несколько или бесконечно
много точек перегиба.
15.Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
Определение 7.1 Вертикальной
асимптотой графика
функции ![]() называется
вертикальная прямая
называется
вертикальная прямая ![]() ,
если
,
если ![]() или
или ![]() при
каком-либо из условий:
при
каком-либо из условий: ![]() ,
, ![]() ,
, ![]() .
Заметим, что мы при этом не требуем,
чтобы точка
.
Заметим, что мы при этом не требуем,
чтобы точка ![]() принадлежала
области определения функции
принадлежала
области определения функции ![]() ,
однако она должна быть определена по
крайней мере в какой-либо из односторонних
окрестностей этой точки:
,
однако она должна быть определена по
крайней мере в какой-либо из односторонних
окрестностей этой точки: ![]() или
или ![]() ,
где
,
где ![]() .
.
Определение 7.2 Наклонной
асимптотой графика
функции
при ![]() называется
прямая
называется
прямая ![]() ,
если выполнены два условия:
1)
некоторый луч
,
если выполнены два условия:
1)
некоторый луч ![]() целиком
содержится в
целиком
содержится в ![]() ;
2)
расстояние по вертикали между графиком
и прямой стремится к 0 при
:
;
2)
расстояние по вертикали между графиком
и прямой стремится к 0 при
:
|
(7.1) |
Наклонной
асимптотой графика
функции
при ![]() называется
прямая
,
если
1)
некоторый луч
называется
прямая
,
если
1)
некоторый луч ![]() целиком
содержится в
;
2)
расстояние по вертикали между графиком
и прямой стремится к 0 при
:
целиком
содержится в
;
2)
расстояние по вертикали между графиком
и прямой стремится к 0 при
:
![]()
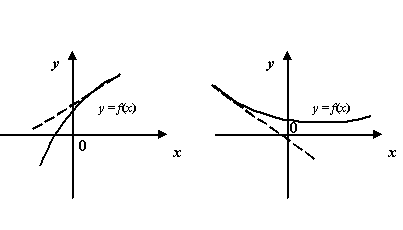
Рис.7.6.Графики функций, имеющие наклонные асимптоты при и при
В
случае, если наклонная асимптота
расположена горизонтально, то есть
при ![]() ,
она называется горизонтальной
асимптотой.
Таким образом, горизонтальная асимптота --
частный случай наклонной асимптоты;
прямая
,
она называется горизонтальной
асимптотой.
Таким образом, горизонтальная асимптота --
частный случай наклонной асимптоты;
прямая ![]() является
горизонтальной асимптотой
графика
при
или
,
если
является
горизонтальной асимптотой
графика
при
или
,
если
![]()
Или
![]() соответственно.
соответственно.
