МАТЕМАТИЧНИЙ АНАЛІЗ

Запитання до екзаменів і заліків (заочне відділення)

Теоретичні запитання

«Елементи теорії множин. Потужності. Теорія дійсних чисел.»

1. Множини і операції над ними. Властивості операцій над множинами. Закони двоїстості.

2. Загальне поняття функції (відображення). Поняття зворотного відображення.

3. Еквівалентні (рівнопотужні) множити. Приклади.

4. Принцип повної математичної індукції.

5. Поняття зчисленної множини. Властивості зчисленних множин.

6. Числова вісь і нескінчені десяткові дробі. Теорема про незчисленність відрізка [0,1].

7. Потужність континуума. Властивості множин потужності континуума.

8. Порівняння потужностей.

9. Множина раціональних чисел і її властивості. Зображення раціональних чисел на числовій прямій

10. Упорядкування множини нескінченних десяткових дробів.

11. Множини нескінченних десяткових дробів обмежені зверху (знизу). Верхня, нижня, точна верхня, точна нижня межі множин нескінченних десяткових дробів. Теорема про існування точних меж.

12. Наближення дійсних чисел раціональними.

13. Операція додавання нескінченних десяткових дробів. Операція добутку нескінченних десяткових дробів.

14. Множина дійсних чисел і її властивості.

15. Основні числові нерівності з модулями. Деякі конкретні множини числової прямої (сегмент, інтервал, півсегмент, числова пряма, півпрямі відкриті і замкнені, 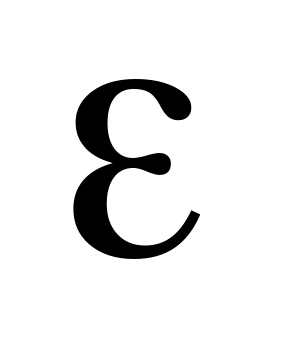-окіл точки, окіл точки).

«Теорія послідовностей»

16. Нескінченно мала і нескінченно велика послідовності. Властивості послідовності x_n=qⁿ в залежності від q.

17. Обмежені і необмежені послідовності. Обмеженість нескінченно малої послідовності. Необмеженість нескінченно великої послідовності.

18. Дії над нескінченно малими послідовностями (сума, добуток). Зв’язок між нескінченно малою і нескінченно великою послідовностями.

19. Три еквівалентні означення збіжної послідовності. Теорема про єдиність границі збіжної послідовності. Зв’язок між збіжністю та обмеженістю послідовності.

20. Арифметичні операції над збіжними послідовностями.

21. Теореми про граничний перехід під знаком нерівності.

22. Поняття монотонної і строго монотонної послідовностей. Теорема про збіжність монотонної обмеженої послідовності (теорема Вейєрштрасса).

23. Принцип стяжних сегментів.

24. Числа е.

25. Поняття підпослідовності числової послідовності. Означення граничної точки

26. Поняття верхньої та нижньої границі і теорема про їх існування для обмеженої послідовності. Теорема Больцано-Вейєрштасса.

27. Поняття фундаментальної числової послідовності. Критерій Коші збіжності числової послідовності Приклад.

«Границя функції однієї змінної»

28. Способи задання функцій. Означення границі функції в точці за Гейне і за Коші та їх еквівалентність. Приклади.

29. Односторонні границі функції в точці. Приклади. Необхідні і достатні умови існування границі функції в точці.

30. Границі функції на нескінченності. Приклади.

31. Арифметичні операції над функціями, що мають границю. Приклади.

32. Перша істотна границя.

33. Наслідки з першої істотної границі.

34. Друга істотна границя.

35. Наслідки з другої істотної границі.

36. Нескінченно малі функції в точці та їх порівняння. Приклади. Властивості 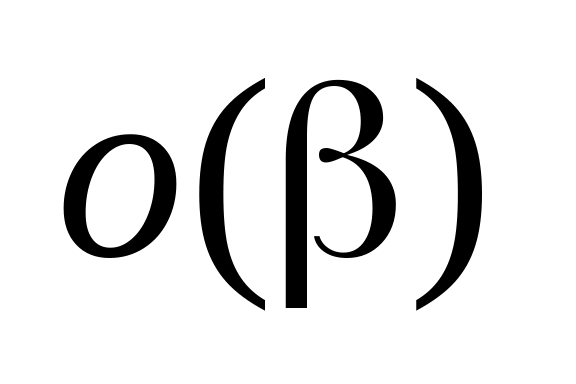. Властивості еквівалентних нескінченно малих функцій.

37. Нескінченно великі функції в точці та їх порівняння. Приклади.

«Неперервність функцій однієї змінної»

38. Різні означення неперервності функції в точці. Означення односторонньої неперервності. Критерій неперервності функції в точці, виражений через односторонні границі.

39. Арифметичні операції над неперервними функціями. Складна функція і її неперервність.

40. Неперервність тригонометричних функцій. ( . Графічне зображення цих функцій.

41. Неперервність функцій . Графічне зображення цих функцій.

42. Неперервність функцій та їх графічне зображення.

43. Класифікація точок розриву. Приклади. Кусково неперервні функції.

44. Локальні властивості неперервної функції в точці (локальна обмеженість, сталість знаку).

45. Глобальні властивості неперервності функції на відрізку. Теорема Коші про проходження неперервної на відрізку функції через нуль при зміні знаку. Теорема про проходження неперервної функції через будь-яке проміжне значення.

46. Неперервність оберненої до монотонної неперервної на відрізку функції.

47. Перша і друга теореми Вейєрштрасса.

48. Означення рівномірної неперервності на множині і його відмінність від означення неперервності функції на множині . Приклади.

49. Теорема Кантора. Приклади щодо її застосування. Поняття коливання функції на відрізку. Наслідок з теореми Кантора.

«Диференціальне числення функцій однієї змінної»

50. Поняття похідної функції в точці (приріст функції, різницева форма неперервності функцій, різницеве відношення, означення похідної функції в точці), правої і лівої похідної. Необхідні і достатні умови існування похідної функції в точці.

51. Геометричний і фізичний зміст похідної функції в точці

52. Похідні від функцій за означенням.

53. Лема про неперервність в точці функції, що має похідну в цій точці. Арифметичні операції над похідними.

54. Похідна складної функції і оберненої

55. Похідні від функцій з використанням теорем про арифметичні операції над функціями і про похідну від складної функції і оберненої.

56. Логарифмічне диференціювання. Приклади.

57. Диференційованість та диференціал функції в точці. Означення. Необхідні і достатні умови диференційованості функції в точці. Геометричний зміст диференціалу.

58. Використання диференціалу для наближених обчислень. Інваріантність форми першого диференціалу. Таблиця диференціалів.

59. Похідні вищих порядків. Означення, приклади.

60. Виведення формули бінома Ньютона за допомогою похідної.

61. Формула Лейбниця.

62. Диференціали вищих порядків. Неінваріантність форми диференціалів вищих порядків.

63. Диференціювання функцій, що задані параметрично , неявно. Приклади.

64. Означення монотонної функції в точці. Поняття локального екстремуму. Достатні умови монотонності функції в точці. Теорема Ферма та її геометричний зміст.

65. Теореми Ролля, Лагранжа і Коші та їх геометричний зміст.

66. Наслідки з теореми Лагранжа. Теорема про постійність функції, що має на інтервалі рівну нулю похідну та її геометричний зміст. Необхідні і достатні умови не зростання (не спадання) функції на інтервалі.

67. Перше правило Лопіталя.

68. Друге правило Лопіталя.

69. Перша і друга достатні умови екстремуму функції в точці.

70. Опуклі функції. Означення. Геометричний зміст. Критерій опуклості вниз.

71. Точки перегину. Означення. Необхідні умови перегину. Достатні умови перегину.

72. Асимптоти графіка функції.

73. Схема побудови графіка функції за допомогою похідної. Приклад.

74. Пошук найбільшого і найменшого значень функції на відрізку. Приклад.

75. Формула Тейлора для многочленів.

76. Формула Тейлора довільної функції з залишковим членом в формі Пеано.

77. Прилади розкладу функцій за формулою Тейлора з залишковим членом в формі Пеано. Єдність представлення функцій з точністю до нескінченно малого порядку, вище за .

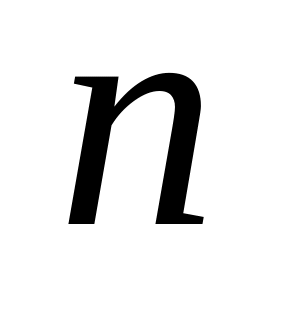78. Форми залишкового члену у формулі Тейлора. Приклади.