Оглавление

ГЛАВА 3. ЛОГИКА

§ 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ЛОГИКИ. БУЛЕВА АЛГЕБРА

§ 2. ИНВЕРСИЯ (ЛОГИЧЕСКОЕ ОТРИЦАНИЕ)

§ 3. КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ)

§ 4. ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ)

§ 5. ИМПЛИКАЦИЯ (ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ)

§ 6. ЭКВИВАЛЕНЦИЯ (ЛОГИЧЕСКОЕ ТОЖДЕСТВО)

§ 7. ТАБЛИЦЫ ИСТИННОСТИ

§ 8. ЛОГИЧЕСКИЕ ФОМУЛЫ. ЗАКОНЫ ЛОГИКИ

§ 9. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ

Упрощение и преобразование формул.

Задачник

§ 10. РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ

I. Решение логических задач средствами алгебры логики.

II. Решение логических задач табличным способом.

III. Решение логических задач с помощью рассуждений.

IV. Задачник логика

§ 1. Основные определения логики. Булева алгебра

Логика – это наука о формах и способах мышления.

Мышление всегда осуществляется в каких-то формах – понятиях, высказываниях, умозаключениях, логических выражениях и т.д.

Понятие – форма мышления, фиксирующая основные признаки предмета.

Высказывание (суждение) – это предложение, в котором что-то отрицается или утверждается о предмете, его свойствах или отношениях между предметами.

Логическое выражение – это либо одно высказывание, либо несколько высказываний, соединенных логическими операциями.

Умозаключение – форма мышления, с помощью которой из одного или нескольких суждений (посылок), можно получить новое суждение (заключение).

Алгебра высказываний (Булева алгебра) была разработана для того, чтобы можно было определять ложность/истинность высказываний, не вникая в их содержание. В соответствие суждению (простому высказыванию)

ставятся логические переменные (прописные буквы латинского алфавита).

Рассмотрим простое высказывание:

A = «Дважды два равно четырем»

B = «Дважды два равно пяти»

О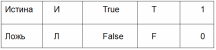 чевидно, что высказывание А – истинно, а высказывание В – ложно. Существуют разные варианты обозначения истинности и ложности переменных:

Иными словами, «А =1, В = 0».

В булевой алгебре мы можем также проводить над высказываниями определенные логические операции, в результате которых, получаются новые, составные высказывания. Наиболее часто используются логические связки «и, или, не». Они заменяются логическими операциями «инверсия, конъюнкция, дизъюнкция», соответственно. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

§ 2. Инверсия (логическое отрицание)

В обыденной речи мы часто пользуемся словом "не", или словами "неверно, что", когда хотим что-то отрицать.

Пусть, например, кто-то сказал: "Тоска зеленая" (Обозначим это высказывание А). Если Вы не согласны, Вы скажете: " Тоска не зеленая" Или: " Неверно, что тоска зеленая" (Ваше высказывание обозначим В).

Нетрудно заметить, что значения истинности высказываний А и В находятся в определенной связи: если А истинно, то В ложно, и наоборот.

Операция, с помощью которой из высказывания А получается высказывание В называется логическим отрицанием (инверсией), и само высказывание В называется отрицанием высказывания А и обозначается Ā . Итак,

Инверсия (логическое отрицание) – это составное высказывание, образованное отрицанием. Инверсия делает истинное высказывание ложным, а ложное истинным. Существуют специальные обозначения для этой функции:

Ā, ¬А, not A , не А

Из приведенной ниже таблицы истинности мы видим, как изменяются переменные, в зависимости друг от друга:

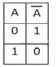
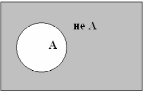
То есть, существует множество А. Все, что находится в пределах этого множества – истина. Все, что за его пределами – отрицание истины – ложь:

Пример 1: пусть высказывание А – 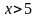, тогда составное высказывание Ā – .

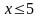Пример 2: пусть высказывание А – , тогда составное высказывание Ā – .