56. Стационарные цепи Маркова

Всякое неотрицательное решение , удовлет­воряющее условию нормировки, принято называть стационарным, или инвариантным, распределением вероятностей Марковской цепи с матрицей переходных вероятностей .

Опр. Набор чисел называется стацио­нарным распределением цепи Маркова с дискретным време­нем, если:

1) является распределением вероятностей, т.е. .

2) имеет место равенство .

В частности, если начальное распределение совпадает со стационарным, то на любом шаге цепь Маркова будет иметь стационарное распределение, поэтому такая цепь Маркова называется стационарной.

Т.1 (эргодическая теорема Маркова- Бернштей-на). Если существуют такие и , что выполня­ется неравенство ,то цепь Маркова является эргодической; существует единственное стационарное распределение этой цепи, совпадающее с эргодическим.

Опр. Цепь Маркова с дискретным временем назы­вается неприводимой, если такое, что .

Т.2 (эргодическая теорема Феллера). Неприводи­мая апериодическая цепь Маркова относится к одному из следую­щих двух классов:

а) все состояния цепи невозвратны (либо нулевые), в этом

случае , и не существует стационарного распределения цепи;

б) все состояния цепи положительны, в этом случае

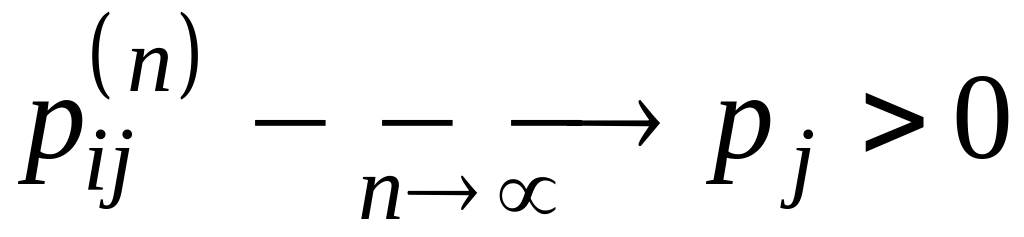при этом является стационарным распределением цепи и не существует других ее стационарных распределений.

Т.3 (эрг-кая т. Фостера). Для того чтобы неприводимая апериодическая цепь Маркова была эргодич-на, необходимо и достаточно, чтобы система уравнений 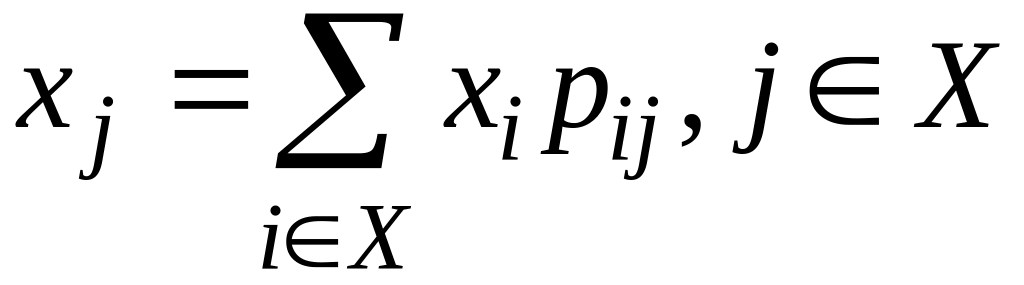имела нетривиальное решение , такое, что При этом существует единственное стационарное распределе­ние, которое совпадает с эргодическим.

Теорема 10.10 (эрг-кая т. Маркова). Для того, чтобы неприводимая апериодическая цепь Маркова была эргодична, достаточно существования , натурального числа i₀ и набора неотрицательных чисел х₀,х₁,х₂,... таких, что для , для .

При этом существует единственное стационарное распределе­ние, совпадающее с эргодическим.

57. Оптимальные стратегии в марковских цепях

Рассмотрим цепь Маркова с конечным множеством состояний и матрицей вероятностей переходов . Пусть при переходе из состояния . в состояние i_k мы получаем некоторое вознаграждение r_jk . Например, пусть , - раз­личные места в городе; переход из в i_k означает перевозку пас­сажиров такси по данному маршруту; тогда - это прибыль, входящая в плату за проезд из ( ) в (i_k). Найдем общее вознаг­раждение, которое следует ожидать после переходов цепи Марко­ва за п шагов.

Предположим, что цепь Маркова находится в состоянии и пусть - суммарное среднее вознаграждение за п шагов, если вначале цепь находилась в состоянии . Тогда средний выигрыш после первого шага. Если после первого шага цепь Маркова находится в состоянии , то средний выигрыш на оставшихся п-1 шагах составит . Поэтому полный сред­ний выигрыш за п шагов равен .

Введем матричные обозначения , .

Тогда в матричной форме последнее соотношение может быть пе­реписано как

V(n) = Q + PV(n-1).

В стационарном режиме среднее вознаграждение за один шаг может быть найдено в виде 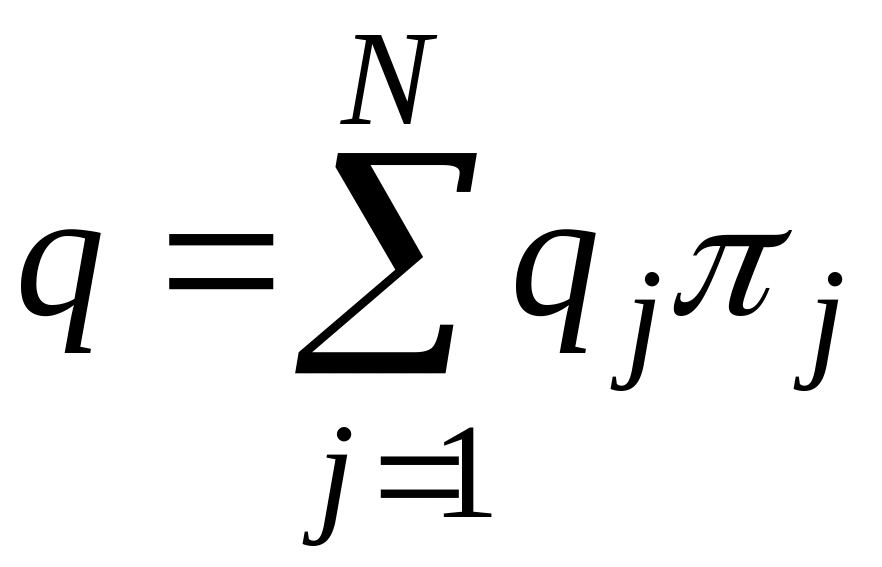, (10.22) где , финальные вероятности состояний.