53. Классификация состояний по асимптотическим свойствам переходных вероятностей

Используя марковское свойство, можно показать что (1). Для каждого состояния введем величину , которая является вероятностью того, что цепи Маркова, выходящая из состояния , рано или поздно вернется в это состояние.

Опр.: Состояние называется возвратным, если , и невозвратным, если . Каждое возвратное состояние можно отнести к одному из двух типов в зависимости от величины среднего времени возвращения (от его конечности или бесконечности). Величина по определению математического ожидания равна среднему числу шагов, за которые цепи Маркова возвращается в состояние , т.е. для цепи с дискретным временем характеризует среднее время возвращения в состояние . Величина характеризует интенсивность возвращения в состояние.

Опр.: Возвратное состояние называется положительным, если , и нулевым, если .

Т.1(критерий возвратности состояний). Состояние возвратно тогда и только тогда, когда (2). Если состояние возвратно и , то состояние также возвратно.

Д-тво: Из (1) следует , и, значит, . Поменяем местами индексы суммирования. Имеем

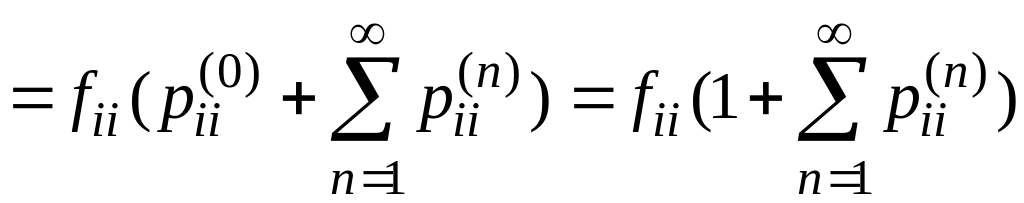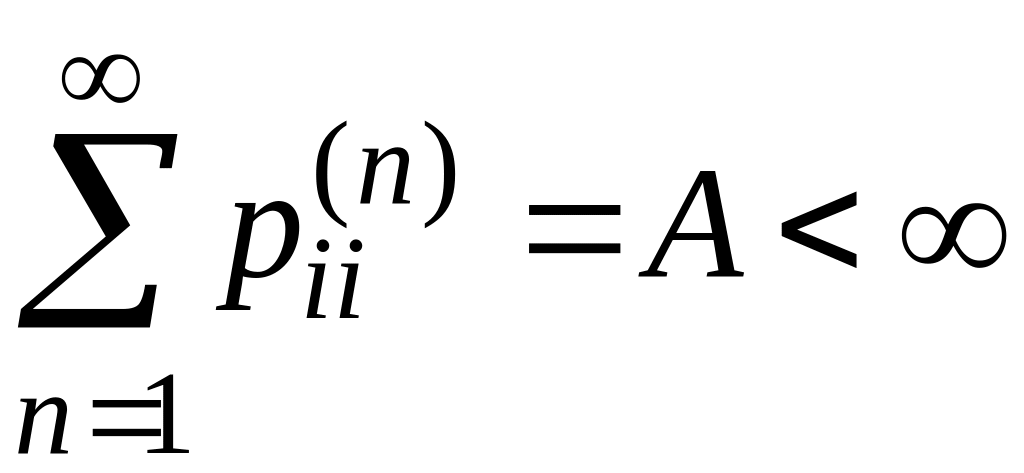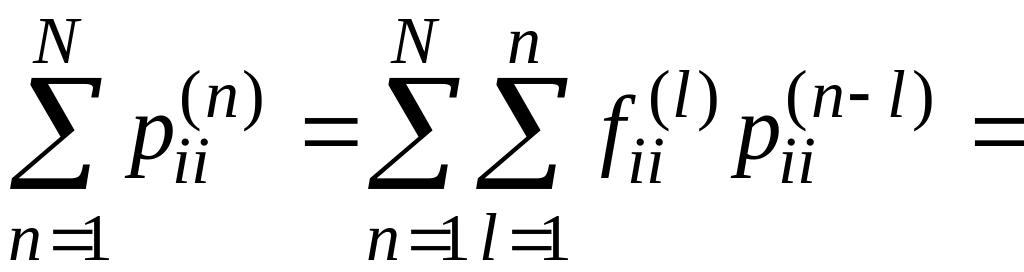
. Отсюда следует, что если , то , и поэтому состояние невозвратно. Пусть выполняется соотношение (2). Тогда для . Поэтому , откуда получаем . Итак, если (2) выполнено, то , т.е. состояние возвратно.

Т.2: Если состояние невозвратно, то для любого , и, значит, .

Т.3: Все состояния апериодической неразложимой цепи Маркова возвратны.

54.Эргодические цепи Маркова

Многие Марковские цепи обладают свойством эргодичности: пределы не только существуют, не зависят от , образуют распределение вероятностей, т.е. , но и таковы, что . Такие распределения , называются эргодическими.

Опр.: Цепь Маркова с дискретным временем называется эргодической, если .

Теорема (эргодическая теорема для цепей Маркова с дискретным временем и конечным числом состояний). Пусть . Тогда: 1) если такое, что (1), то числа такие, что (2) и (3); 2) числа удовлетворяют системе уравнений . (4)

Док-во: Введем обозначения . Т.к. , то , откуда , а также , т.е. наибольшая из вероятностей с ростом не может возрастать, а наименьшая не может убывать. Покажем , тогда (3) выполняется. Для этого покажем, что . (5)

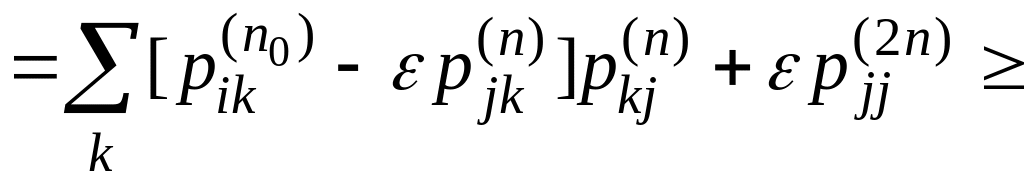
Пусть согласно (1). Тогда . Откуда . Также покажем . Объединяя эти неравенства, получаем и, следовательно, . Для некоторой подпоследовательности , и т.к. разность монотонна по , то соотношение (5) выполняется, следовательно имеет место соотношение (3). При , откуда .

Докажем вторую часть теоремы. Запишем прямое уравнение Чепмена-Колмогорова . Тогда и, используя (3), получаем систему уравнений (4).

55. О средних временах переходов между состояниями

Обозначим через Е_к мн-во состояний к -го эргодического класса, Q - множество несущественных состояний, -сред­нее время перехода из i-го несущественного состояния, , в -й эргодический класс. Найдем это время. Цепь Маркова за один шаг может перейти из i -го несуществен­ного состояния в некоторое состояние с вер-тью ,

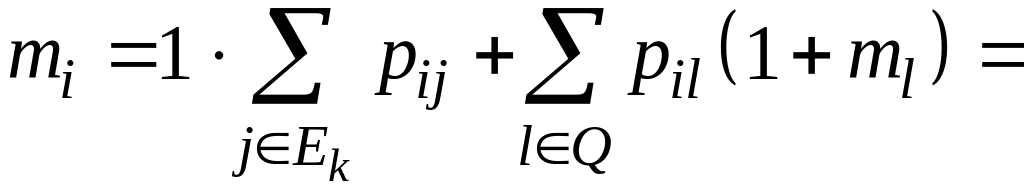
тогда время перехода равно 1. Если же цепь за первый шаг перейдет в другое состояние вероятностью , то среднее время пере­хода в эргодический класс будет равно , и окончательно имеем (10.20)

Решая эту систему ур-ний относительно , полу­чим нужные нам средние времена. Если нас интересуют средние времена перехода в каждый эр­годический класс, то систему уравнений (10.20) удобно записать в матричном виде. Обозначим , , .

Учитывая, что в этом случае =1, имеем , т.е. , где I - единичная матрица. Последнее соотношение и определяет вектор среднего времени перехода из несущественного состояния в эргодические классы.

Рассмотрим теперь среднее время перехода из состояния в состояние внутри класса. Пусть Е - множество состояний одного класса . Через обозначим среднее число шагов, необхо­димых для переходов из i -го состояния в j-е состояние. За один шаг цепь может из i -го состояния с вероятностью перейти в j-е состояние, тогда время перехода будет равно 1, и оно будет равно 1 + m_kj, если за этот шаг цепь перейдет из i -го состояния в некоторое промежуточное k -е состояние. Тогда по формуле для условного мат. ожидания имеем или .(10.21)

Введем матричные обозначения , , ,

где r - число состояний данного класса. Тогда систему ур-ний (10.21) можно переписать в матричном виде М = S + РМ -PD, откуда получаем . Эта формула определяет искомые средние значения времени пере­хода из одного состояния в другое. Выясним теперь, что собой представляют диагональные элемен­ты матрицы D. Для этого умножим систему уравнений (10.21) на финальную вероятность i-го состояния и просуммируем по i:

Тогда с учетом (10.17) имеем

откуда находим .
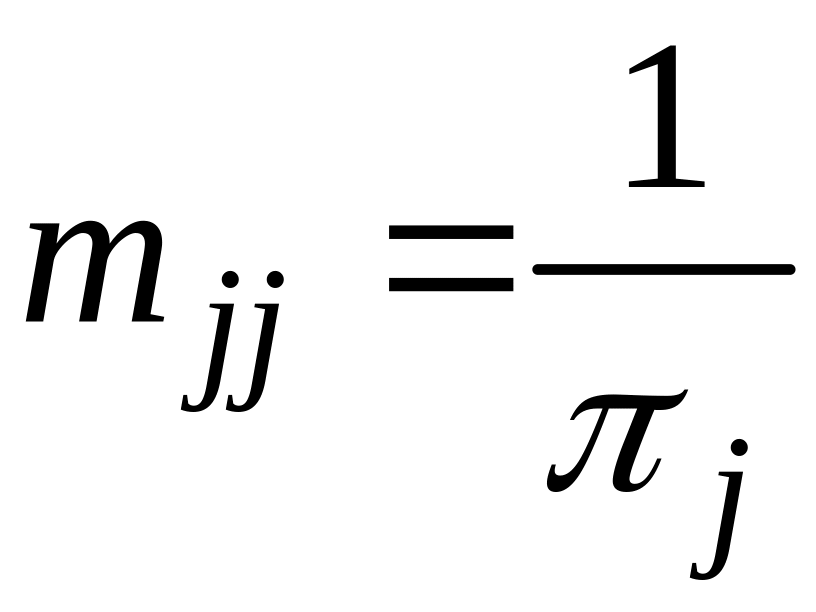