47. Винеровский случайный процесс.

Опр. Однородный гауссовский процесс с независимыми приращениями ξ(t), для которого

называется винеровским (или процессом броуновского движения).

Ковариационная функция такого процесса при t₁<t₂ имеет вид

Отсюда следует, что винеровский процесс является непрерывным, но не является дифференцируемым в среднем квадратичном.

Ковариационная матрица винеровского процесса записывается в виде:

Опр. Винеровский процесс, у которого σ=1, ξ(0)=0, называется стандартным винеровским процессом и обозначается W(t).

n-мерная плотность распределения винеровского процесса имеет вид

48. Марковские случайные процессы и цепи маркова определения.

Пусть задано n+1 сечение процесса ξ(t₁), ξ(t₂),…, ξ(t_n+1) в моменты t₁<t₂<…<t_n+1. Рассмотрим условную плотность вероятностей

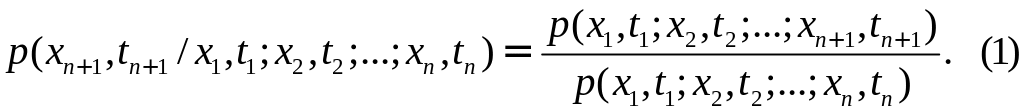
Случайный процесс ξ(t) называется марковским, если его условная плотность распределения (1) не зависит от значений процесса в моменты t₁ ,t₂,…,t_n+1, а определяется лишь значением ξ(t_n)= x_n, т.е.

Эту условную условную плотность вероятностей называют вероятностью перехода системы из состояния x_n в котором она находилась в момент времени t_n, в состояние x_n+1 в момент времени t_n+1>t_n и обозначают

Опр. Случайный процесс ξ(t) , со значениями в Х называется марковским, если и любых борелевских множеств В₁,В₂,…,В_n-1, B_n+1 из R при фиксированном борелевском множестве B_n и фиксированном событии выполняется следующее соотношение

При этом очевидно, что

Опр. Если множество счетно или конечно, то Марковский процесс называется цепью Маркова. Множество значений цепи Маркова Х называют фазовым пространством или пространством состояний цепи Маркова.

Опр. Цепь Маркова у которой множество Т дискретно, называется цепью с дискретным временем, а цепь Маркова у которой Т - некоторый интервал положительной длины, называется цепью с непрерывным временем. Для цепи Маркова с дискретным временем можно записать

где состояние цепи Маркова в некоторый дискретный момент времени t_n.

Опр. Если множество событий Х непрерывно и система переходит из состояния в произвольные моменты времени из множества Т, то соответствующий процесс называется непрерывным марковским процессом.

49. Однородные цепи Маркова.

Рассмотрим цепь маркова с дискретным временем с конечным числом состояний X={1,2,…,N}. Вероятности

называются вероятностями перехода цепи Маркова за n шагов, а просто матрицей перехода. Матрица вида

называется матрицей вероятностей перехода цепи Маркова. Сумма элементов в каждой строке этой матрицы равна 1, т.е. 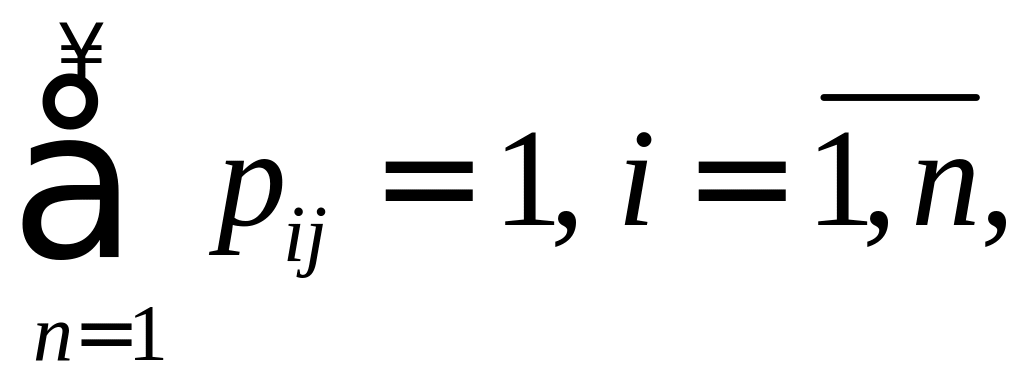т.к. за один шаг цепь Маркова остается в своем состоянии, либо переходит в какое-то иное состояние . Пусть вероятность состояния i на нулевом шаге; набор называется начальным распределением цепи Маркова.

Опр. Если вероятности перехода (1) не зависят от m, то цепь Маркова называется однородной.

Свойства однородных Марковских цепей полностью определяются начальными распределениями и вероятностями перехода p_ij. Для описания эволюции цепи вместо явного выписывания матрицы P=|| p_ij|| используют ориентированный граф,

вершинами которого являются состояния из множества Х, а стрелка означает, что из состояния i возможен переход в состояние j с вероятностью p_ij; в том случае, когда p_ij=0, соответствующая стрелка не проводится.

Опр. Если вероятности перехода

Не зависят от s, то цепь Маркова с непрерывным временем называется однородной.