36. Определение случайного процесса.

При изучении различных реальных явлений рассматривают всевозможные величины, зависящие от времени: x=x(t). Такие величины принято называть процессами. Говоря о случайных про­цессах, как правило, имеют в виду некоторую СВ ξ(t) меняющу­юся с течением времени t. Будем называть случайным процессом ξ(t) функцию от действительного параметра t T (времени), зна­чения которой при каждом t являются СВ. Строгое определение случайного процесса состоит в следую­щем.

Опр. Набор ξ(t)={ξ(t,w), t T, ω Ω} СВ, опреде­ленных на одном и том же вероятностном пространстве (Ω,F, Р), называется случайной функцией.

Опр. Пусть (Ω,F, Р) - вероятностное прост-во, Т - некоторое множество моментов времени. И пусть каждому ω Ω поставлена в соответствие функция ξ_l=ξ(t)=ξ(t,w), t T, со значениями в п -мерном пространстве (n > 1) такая, что при каж­дом фиксированном t T, функция ξ(t,w) является СВ. Эта функ­ция называется случайным процессом.

Следовательно, случайный процесс - это совокупность СИ, зависящих от времени. Естественно, его можно рассматривать кик функцию двух переменных: t и ω . Как следует из определения, ξ(t,w) является n-мерной СВ при любом фиксированном t.

Опр. При фиксированном ω Ω функция ξ(t,w) называется реализацией (траекторией или выборочной функцией) случайного процесса. Совокупность всех реализаций случайного процесса называется ансамблем (семейством) реализаций.

Опр. Случайный процесс ξ(t), t T у которого мн-во Т не более чем счетно, наз-я процессом с диск­ретным временем или случайной последовательностью. Если мно­жество Т совпадает с промежутком прямой, например, Т-[0;+∞) , то ξ(t) наз-ся процессом с непрерывным временем.

Опр. При фиксированном t для случайного процесса ξ(t,w) получаем СВ, которую назовем сечением случайного процесса в момент времени t.

Опр. Пусть t₁ <t₂ < …<t_n - некоторые фиксирован­ные моменты времени. Рассмотрим n-мерную СВ (ξ(t₁), ξ(t₂),..., ξ(t_n)). Распределение вероятностей этой СВ назы­вается п-мерным распределением вероятностей случайного про­цесса, а ф.р. этой СВ

соответственно п -мерной ф.р. случайного процесса

Опр. Случайным процессом ξ(t), заданным на мно­жестве Т, t T наз-ся семейство распределений (6.7), удов­летворяющее условиям согласованности. Набор функций для n=1,2,... называют конечномерными распределениями случайного процесса.

Опр. Если существует неотрицательная функция , такая, что

То она наз-ся n-мерной плотностью распределения случайного процесса.

Характеристическая функция конечномерного распределения:

37. Статистические средние характеристики случайных процессов.

Опр. Средним значением случайного процесса ξ(t) m_ξ(t) наз-ся математическое ожидание случайного процесса в момент времени t:

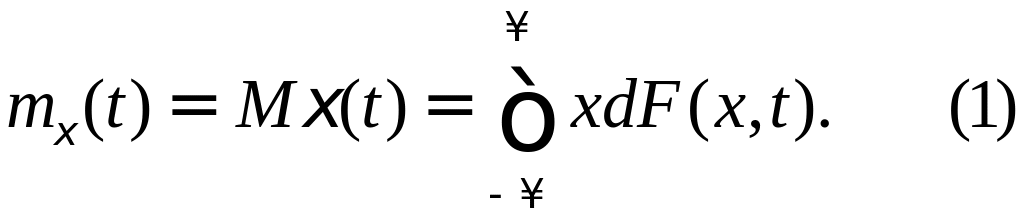
Оно определяется одномерной функцией распределения F(x,t).

Опр. Дисперсией случайного процесса ξ(t) наз-ся дисперсия сечения случайного процесса, которая так же определяется одномерным распределением:

Опр. Корреляционной функцией случайного процесса ξ(t) наз-ся математическое ожидание произведения двух сечений случайного процесса в моменты времени t₁, t₂:

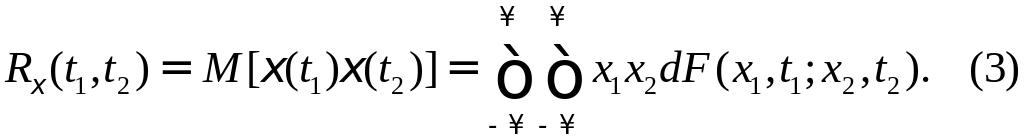
Опр. Ковариационная функция случайного процесса ξ(t) – это математическое ожидание произведения центрированных сечений процесса в моменты времени t₁, t₂:

Величину

Называют нормированной ковариационной функцией, или коэффициентом корреляции случайного процесса. При t₁=t₂=t ковариационная функция совпадает с дисперсией случайного процесса:

Для двух случайных процессов ξ(t) и η(t) вводится понятие взаимной функции корреляции, или кросс-корреляции:

а совместная ковариационная функция двух случайных процессов определяется как матричная функция

Свойства корреляционной функции:

1. Корреляционная функция является симметричной функцией своих аргументов R_ξ(t₁,t₂)= R_ξ(t₂,t₁).

2. .

Док-во. Следует из нер-ва Коши-Буняковского для мат. ожиданий M²(uv)≤Mu²Mv². Обозначив в нем u= ξ(t₁),

v= ξ(t₂), имеем M²[ξ(t₁) ξ(t₂)]= Mξ²(t₁) Mξ²(t₂).

3. Корреляционная функция случайного процесса является положительно определенной, т.е. n и действительных λ₁, λ₂,…, λ_n: .

Док-во. Следует из того, что 4. Пусть Тогда