1.3 Алгоритм построения системы кольцевого тестирования для комбинационных схем.
Рассматривается стандартная реализация КТ комбинационного устройства, имеющего входов и выходов.
Построение теста сводится к выполнению следующих этапов :
Функции объекта тестирования выразим многочленами Жегалкина:
,
.
Для построения КУ найдем сумму функций ДУ:
.
Производим разложение двучлена
по формуле
,
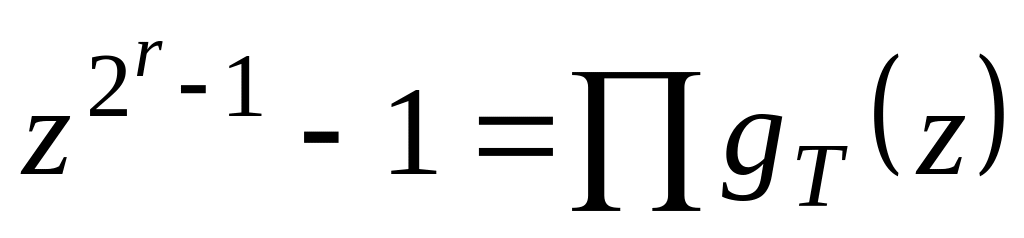соответственно неприводимый над полем
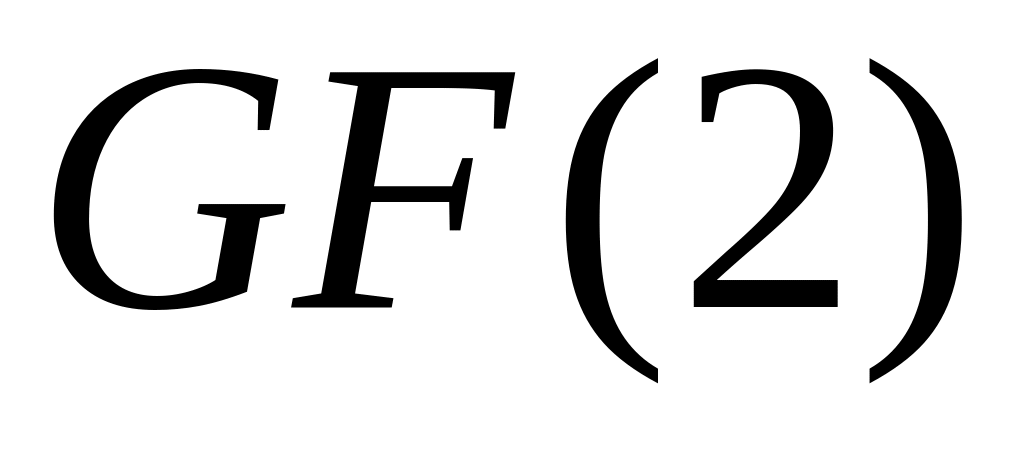многочлен n-ой
степени:
.
Для неприводимого многочлена ой степени
,
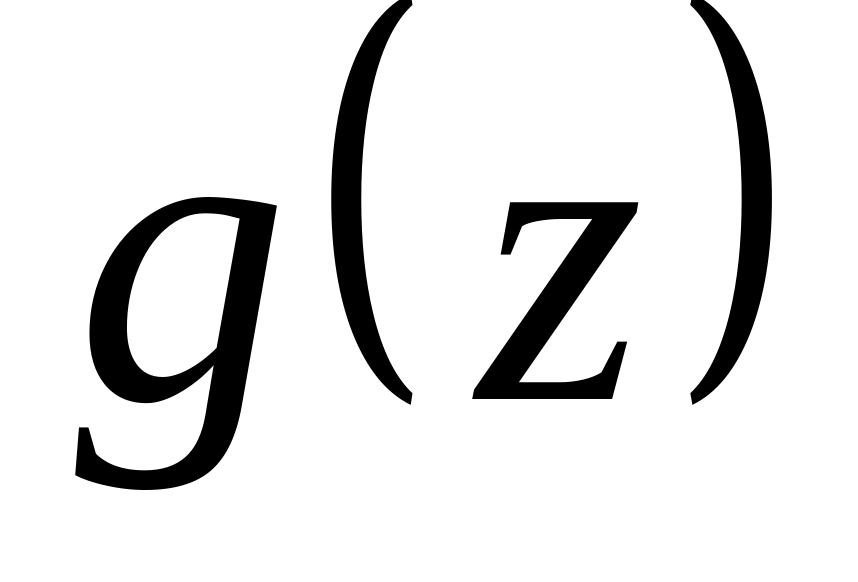принадлежащего показателю
,
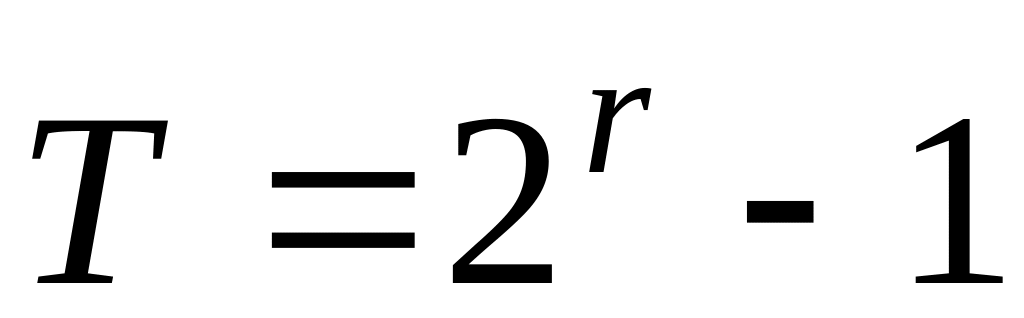необходимо иметь функцию
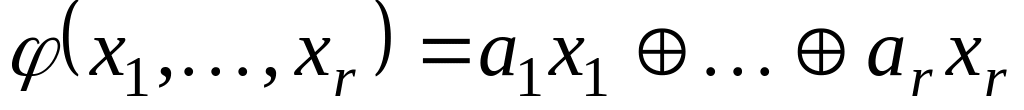.Заданием на синтез КУ служит функция
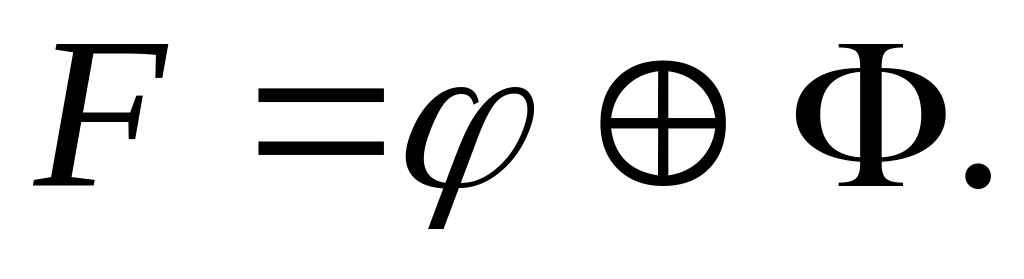По полученному выражению для реализации
КУ используют одну или несколько схем
совпадения и соединений.
Алгоритм представления булевой функции полиномами Жегалкина.
Приведённый выше алгоритм представления булевой функции полиномами Жегалкина является достаточно сложным и некомпактным, отнимающим большое время на осуществление данного представления булевой функции. При многочисленном построении КУ был найден более простой алгоритм представления булевой функции полиномами Жегалкина, позволяющий значительно снизить временные ресурсы на стадии проектирования. Суть данного метода состоит в последовательном применении двух простых действий:
1. Приводим заданную булеву функцию к совершенной конъюнктивной форме. Если булева функция задана в совершенной дизъюнктивной форме, то её следует привести к совершенной конъюнктивной форме путём использования правила Деморгана:
2. Заменяем
все отрицания в совершенной конъюнктивной
форме по формуле
.
Это справедливо, если обратиться к
таблице:
-
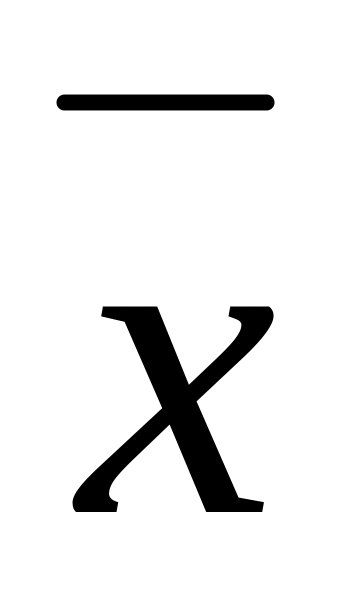
0
1
1
1
0
0
Пример. Представить полиномами Жегалкина булеву функцию:
1. Приводим булеву функцию к совершенной конъюнктивной форме, используя правило Деморгана:
.
2. Заменяем все отрицания на :
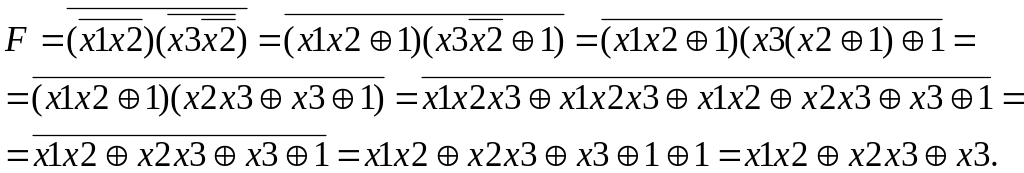
Кольцевое тестирование микросхемы к155ид7.
Для проверки функционирования системы диагностики в качестве объекта тестирования выступала логическая модель интегральной микросхемы К155ИД7. Микросхема К155ИД7 представляет собой дешифратор 3 на 8 и служит для преобразования двоичного трехразрядного кода в один и восьми. Микросхема имеет три адресных входа X0,X1,Х2, управляющие сигналы разрешения-запрещения дешифрации E1-E3 и 8 выходов Y0-Y7. Условное изображение схемы таково:
Рис.6.3: Дешифратор К155ИД7.
Составим по таблице истинности микросхемы К155ИД7 булеву функцию и выразим ее многочленами Жегалкина. Для этого переведем ее из совершенной дизъюнктивной нормальной формы в совершенную конъюнктивную нормальную форму.
Таблица истинности для дешифратора выглядит следующим образом:
Управляющие сигналы |
Входы |
Выходы |
|||||||||||
E1 |
E2 |
E3 |
X0 |
X1 |
X2 |
Y0 |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
Y7 |
1 |
X |
X |
X |
X |
X |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
X |
1 |
X |
X |
X |
X |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
X |
X |
0 |
X |
X |
X |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
;
Необходимо
корректирующее устройство для многочлена
с максимальным для r=3
периодом Т=7. Для этого необходимо иметь
функцию
.
Заданием на синтез корректирующего устройства служит функция
;
По функции F строится КУ:
Рис.6.4: Корректирующее устройство для максимального периода.
Система диагностики выглядит следующим образом:
Рис.6.5: Схема кольцевого тестирования для дешифратора К155ИД7.
Сигналы управления моделью микросхемы и схемой сравнения не вводятся
конечным пользователем в ПЛИС, а логически привязываются к самой системе диагностики при помощи элементов VCC(логическая 1) и GND(логический 0). Перед началом тестирования, при помощи выходного сигнала preset, регистр сдвига логически (без управления ПЛИС) устанавливается в произвольное исходное (начальное) состояние.
Сигналами start и clock запускается процесс тестирования. По истечении 7 тактов работы регистр сдвига, при исправной работе цифровой схемы, должен вернуться в исходное состояние. Проверку этого условия осуществляет схема сравнения, которая сравнивает состояния регистра перед началом тестирования и по его завершению. Низкий уровень выходного сигнала rezsravn (логический 0), свидетельствует об исправном состоянии тестируемой ЦС, и напротив, высокий уровень сигнала (логическая 1), позволяет утверждать, что тестируемая ЦС находится в неисправном состоянии.
Результаты симуляции работы системы диагностики в редакторе временных диаграмм выглядят так:
Рис.6.7: Временные диаграммы тестирования исправной микросхемы К155ИД7.
Как видно из диаграмм, по истечении 7 тактов работы, регистр сдвига возвращается в начальное состояние (на рис.22 это состояние 101). На выходе rezsravn логический 0, т. е. тестируемая модель микросхемы дешифратора исправна.
Теперь искусственно введем ошибку в тестируемую модель дешифратора.
Рис.6.8: Временные диаграммы тестирования неисправной микросхемы К155ИД7.
Как и ожидалось, по истечении 7 тактов работы, регистр не возвращается в свое исходное состояние (на рис.23 исходное состояние 101, конечное - 001). Сигнал rezsravn принимает значение логической 1, таким образом, тестируемая модель дешифратора неисправна.