24

Упругость горных пород

Горные породы считаются твердым упругим телом. Это означает, что после приложения некоторой силы F произойдет деформация объема или формы элементарных ячеек, слагающих породу, а после прекращения действия этой силы F ячейки примут прежний объем и форму. Это явление описывается законом Гука , устанавливающим связь между изменниями размеров элементарной ячейки и значением приложенной силы F на единицу площади (т.е. напряжением). Величина деформации зависит не только от приложенного напряжения, но и от упругих свойств горных пород, которые характеризyются параметрамп Е и σп . Сопротивление пород продольному растяжению или сжатию получило название м о д у л я Ю н г а – Е, который является коэффициентом пропорцио-нальности между напряжением _x (продольно растягивающим или сжимающим) и соот-ветствующей ему продольной деформацией ε:

_x = Е ε = Е · Δl / l ,

где l - длина образца, а Δl - ее изменение. Отношение поперечного сжатия (растяжения) к продольному называется к о э ф ф и ц и е н т о м П у а с с о н а – σ п = (Δd / d)/(Δl / l), где d- ширина образца, Δd- её изменение.

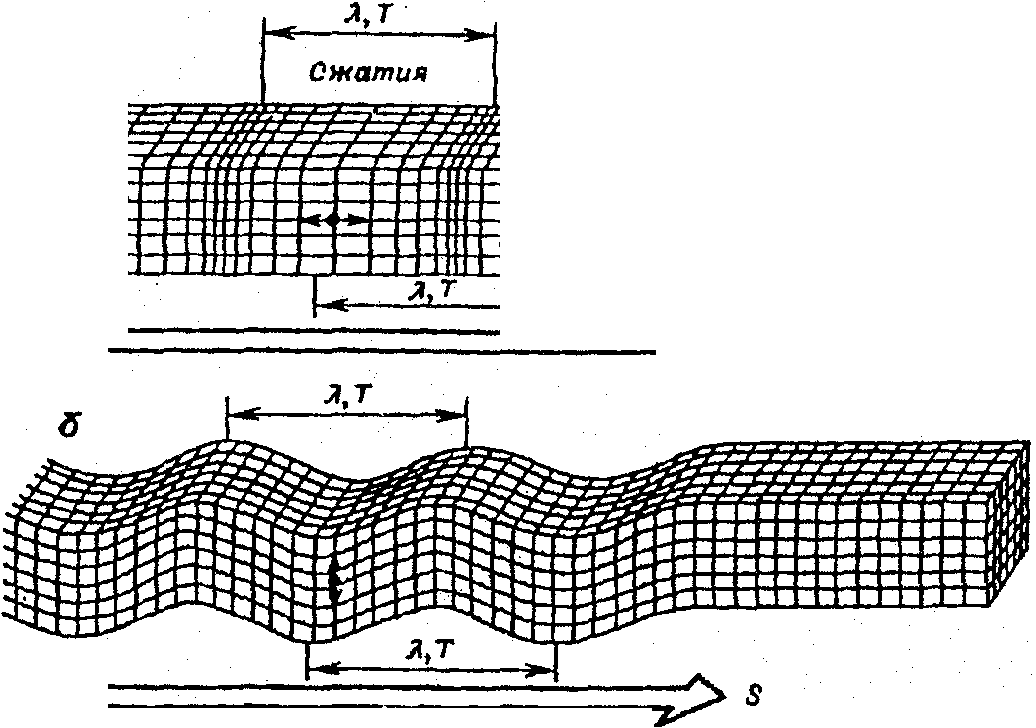
Распространениe деформации в породах создаёт колебания (волны). Движе­ние продольной волны Р представляет собой чередование участков сжатия и растяжения, которые возникают, если имеется источник упругих колебаний (см.рис.34 а,б). Расстояние между ближайшими участками сжатия или растяжения называется д л и н о й волны λ, а время, за которое участок сжатия или растяжения проходит это расстояние, называется п е р и о д о м к о л е б а н и й - Т. Ч а с т о т а f = 1/Т представляет собой число сжатий или растяжений, прошедших через данную точку в 1с. С.к о р о с т ь движения участков сжатия или растяжения зависит от упругих свойств и плотности среды.

Разряжение

Рис.34. Упругие деформации и колебания частиц пород, возникающие при прохождении через них волн: а - продольных Р, б – поперечных S (по Б.А. Бош; 1976 г.)

Под действием приложенных извне сил, вследствие присущей им упругости, породы изменяют свою структуру (форму) и размеры. Однако они способны возвращаться к начальному состоянию после снятия деформировавших их усилий, не превосходящих предела упругости.

Способность горных пород сохранять упругость, передавать упругие деформации с определенной скоростью и поглощать упругую энергию определяется комплексом физических харак­теристик, объединяемых обобщающим понятием – упругие свойства. К числу этих характеристик относятся модули Юнга E, сдвига G, всестороннего сжатия К, скорости распространения продольных Vp, поперечных Vs и поверхностных Vk упругих волн, коэффициенты Пуассона σ_п объемного сжатия β, поглощение продольных, поперечных и поверхностных упругих волн  α_р, α_s и α_r.

Упругость однородно-анизотропных пород описывается бoльшим числом (до 21) независимых коэффициентов упругости, скоростей упругих волн и коэффициентов поглощения.

Модули Е, G и К (Па) являются коэффициентами пропорциональности в уравнениях, связывающих напряжения σ (Па), созданные в породе определенными усилиями с соответст­вующими им деформациями. Напомним, что паскаль (Па) это напряжение, численно равное силе в 1 ньютон, действующей на 1м² площади.

Коэффициент сжимаемости (Па^-1) - это величина, обратная модулю всестороннего сжатия β = l/К, Коэффициент Пуассона σ _п = l₂/ l₁ (где l₂ и l₁ -поперечная и продольная деформации бруска породы, к торцовым граням которого приложены равные растягивающие или сжимающие усилия) характеризует интенсивность поперечных деформаций пород при приложении к образцу продольных усилий.

Скорости Vp,Vs,V_R (м/с) распространения упругих колебаний связаны с временами τ_P, τ_S и τ_R (мкс/м) распространения упругих продольных, поперечных и поверхностных волн в образце породы следующими равенствами. Для продольных волн Vp = l/ τ_P, для поперечных волн V_S = I / τ_S, для поверхностных волн V_R =l / τ_R, где l -длина образца.

При распространении волн любого типа в образце породы их энергия переходит в энергию рассеянных волн и убывает вследствие потерь.

Амплитуда упругой волны изменяется с расстоянием х от точечного источника колебаний, где находится начало отсчета, по закону

- n

A =A₀ (x/x0) e ^{– α (x –x0),}

где A₀ - амплитуда на расстоянии хо от источника, находя­щегося на линии, проходящей через центр источника колебаний и точку х; n - амплитудный показатель расхождения волны от источника в зависимости от типа волны, структуры и степени неоднородности породы; α- амплитудный коэффици­ент поглощения.

В реальных горных породах обнаруживаются одновременно как рассеяние, так и затухание упругой волны, обусловленные их неидеальной упругостью и неоднородностью.

Петрофизические величины, характеризующие упругие свой­ства горных пород, должны быть известны при решении следующих задач.

1. Выяснение строения и напряженного состояния земной коры и верхней мантии методами сейсмологии и глубинного сейсмического зондирования.

2. Исследование послойной зональности упругих свойств осадочных горных пород.

3. Тектоническое районирование.

4. Выяснение механизма распространения, поглощенных уп­ругих волн в горных породах и их деформации при различных видах напряжений.

5. Изучение корреляционных связей между рассматривае­мыми и другими петрофизическими и петрохимическими вели­чинами.

6. Оценка пределов изменения величин, xaрактеризующих упругие свойства различных типов и групп горных пород.

7. Разработка новых модификаций и повышение эффектив­ности имеющихся методов сейсмической разведки и акустичес­ких методов исследования скважин. Расчет и конструирование горных машин и механизмов.

8. Обоснование параметров взрывных работ.

10. Оценка устойчивости массивов пород, обнажаемых гор­ными выработками.

Коэффициенты и модули упругости сухих образцов пород, определенные динамическими способами, изменяются в следую­щих пределах: модуль Юнга Е (<0,3-22)×10¹⁰ Па, модуль сдвига G (<0,1-9)×10¹⁰ Па, модуль всестороннего сжатия K (<0,15-14)×10¹⁰ Па, коэффициент Пуассона σп 0,08-0,42.

Здесь малые значения модулей упругости Е, G и К относятся к рыхлым, большие - к плотным породам. Наименьшие вели­чины σп установлены у преимущественно кварцевых пород (кварцитов и др.). Влажность пород снижает величины модулей и коэффициентов упругости.

Скорость Vp распространения упругих волн в горных породах изменяется от < 300 до 8 000 м/с и более. Скорости Vs и VR варьируют в менее широких пределах. Коэффициенты σ_п поглощения продольных волн при частоте 1 МГц для свежих магматических пород колеблются в пределах 0,8-5 м ^1. Для выветрелых гранитов и граносиенитов σ_п.. выше - от 11 до 14 ^1 .

Еще большие значения для тех же пород имеют коэффициенты поглощения поперечных волн-от 18 до 27 м ^1. В водонасыщенных песках при частоте 30-35 кГц σ_п = 0,21 м ^1, а при частоте 80-90 кГц достигает 1,5 м ^1. В нефтенасыщен­ном песке при тех же частотах его величины соответственно равны 4,2 и 5,6 м ^1.

Величины, характеризующие упругие свойства горных пород, зависят от их состава, структуры, частоты упругих колебаний, температуры и давления.

МОДУЛИ И КОЭФФИЦИЕНТЫ УПРУГОСТИ

Способы определения коэффициентов упругости Е, σ_п, β, К, G подразделяются на статические и динамические.

В статических способах при помощи механических, оптико­-механических, акустических, электромеханических и других тензометров определяются линейные перемещения или дефор­мации при заданных напряжениях сжатия, реже растяжения, изгиба или кручения, по которым рассчитываются коэффици­енты упругости.

В импульсных динамических способах для определения коэффициентов упругости в одном или

двух образцах пород возбуждаются звуковые или ультразвуковые колебания и регистрируются две скорости распространения vp и vp_ст. В неограниченной по размерам породе и в ее стержне Vр и Vs ~ продольных и поперечных колебаний или Vр и VR продольных и поверхностных (релеевских) колебаний. По этим скоростям и плотности сухой породы δ_с, можно рас­считать основные коэффициенты упругости.

Лабораторная работа 1

Определение модулей и коэффнциентов упругости по скоростям

продольиой упругой волны в безграничной породе и ее стержне

Теория. В способе определения коэффициентов упругости по Vp_м И Vp_ст измеряют значения этих скоростей в безграничной породе (массиве) и ее стержне, а также плотность сухой породы δ_с.

Отношение VPст = sqr(E/σ_п) к VP = VPм= sqr(E(1-σ_п)/(δc(1+σ_п)(1-2σ_п))), равное VP ст/ VPм =sqr((1-σ_п-2σ_п²)/(1-σ_п)) позволяет рассчитать коэффициент Пуассона; зная σ_п и δc вычисляют модуль Юнга

Е= V²рм δc (1+ σ_п) (1+2σ_п)(1- σ_п) (34)

по известным Е и σ_п можно определить модуль сдвига, сжимаемость β и модуль всестороннего сжатия К:

(35)

(36)

К = 1/β = Е/3(1-2σ_п) (37),

скорость распространения поперечных волн Vs=sqr (E/2 δc (1- σ_п)) и модуль сдвига G= Vs² δ_с

Аппаратура, оборудование, материалы те же, что и при определении скоростей Vp и Vp_ст расспрос-транения упругих волн (см. ниже).

Порядок выполнения работы. 1. Определение скорости Vp и Vp_ст (см. ниже).