Раздел №1

Исходные данные:

• краткие теоретические сведения,

• вычисление определителя матрицы двумя аналитическими способами,

• вычисление определителя в системе MATLAB,

• вычисление обратной матрицы классическим способом,

• вычисление обратной матрицы в системе MATLAB.

1.краткие теоретические сведения

2.вычисление определителя матрицы двумя аналитическими способами:

1)вычисление определителя классическим методом _{2)вычисление определителя методом разложения по элементам строки и столбца:}

3. вычисление определителя в системе MATLAB

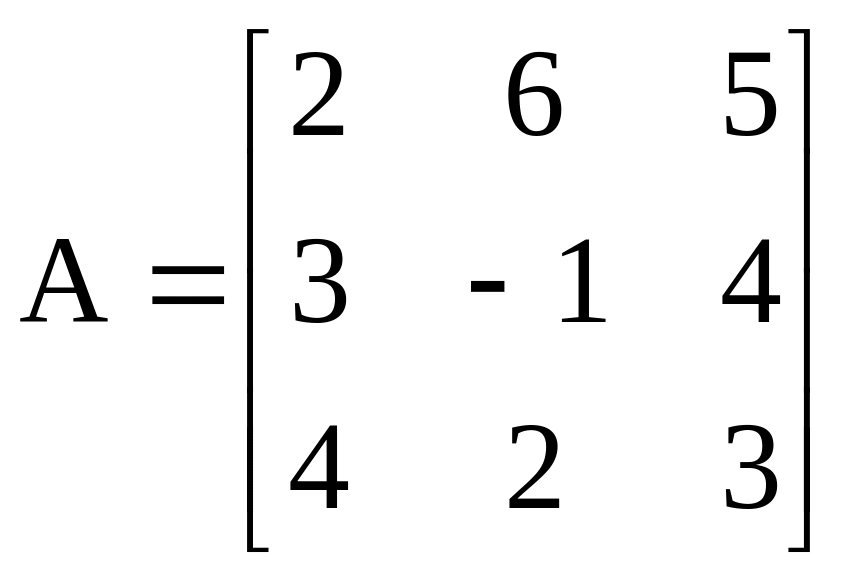
>> A=[2,6,5;3,-1,4;4,2,3];

>> det(A)

ans =

70

4. вычисление обратной матрицы классическим способом

1. Записываем матрицу , транспонированную к матрице .

2. Заменяем каждый элемент матрицы определителем, полученным в результате вычеркивания строки и столбца, на пересечении которых расположен данный элемент.

3. Этот определитель сопровождаем знаком плюс, если сумма индексов элемента четная, и знаком минус – в противном случае.

4. Делим полученную матрицу на определитель матрицы .

5.вычисление обратной матрицы в системе MATLAB

A=[2,6,5;3,-1,4;4,2,3];

>> inv(A)

ans =

-0.1571 -0.1143 0.4143

0.1000 -0.2000 0.1000

0.1429 0.2857 -0.2857

Раздел №2

Расчет установившихся режимов электрических систем

1.схема замещения электрической сети не содержит замкнутых контуров

Индивидуальное задание

Для схемы, представленной на рис.1 найти токи в ветвях разомкнутой электрической сети, используя матричную форму записи 1-го закона Кирхгофа. Токи нагрузки заданы в таблице 1.

Рис. 1

Таблица 1

	А	А	А
26	5+j6

Данный раздел должен содержать:

• краткие теоретические сведения,

• обобщенное уравнение состояния,

• вычисление обратной матрицы для матрицы классическим методом

• вычисление обратной матрицы для матрицы в системе MATLAB

• вычисление токов в ветвях аналитическим методом и с помощью MATLAB- программы,

1.Краткие теоретические сведения

2.обобщенное уравнение состояния

(1)

Уравнение (1) объединяет два матричных уравнения.

Уравнение по первому закону Кирхгофа

.

Уравнение по второму закону Кирхгофа

,

3.вычисление обратной матрицы для матрицы классическим методом

1. Записываем матрицу , транспонированную к матрице _M.

2. Заменяем каждый элемент матрицы определителем, полученным в результате вычеркивания строки и столбца, на пересечении которых расположен данный элемент.

3. Этот определитель сопровождаем знаком плюс, если сумма индексов элемента четная, и знаком минус – в противном случае.

4)Делим полученную матрицу на определитель матрицы _M.

вычислением определитель классическим методом

4. вычисление обратной матрицы для матрицы в системе MATLAB

>> M=[-1,1,1;0,-1,0;0,0,-1];

>> inv(M)

ans =

-1 -1 -1

0 -1 0

0 0 -1

5. вычисление токов в ветвях аналитическим методом и с помощью MATLAB- программы

1) аналитическим методом

2)с помощью MATLAB- программы

>> J=[5+i*6;5+i*6;3+i*4];

>> Minv=[-1,-1,-1;0,-1,0;0,0,-1];

>> -Minv*J

ans =

13.0000 +16.0000i

5.0000 + 6.0000i

3.0000 + 4.0000i

2.схема замещения электрической сети содержит замкнутые контуры

Индивидуальное задание

Для схемы представленной на рис.2 определить токи в ветвях схемы, напряжения в узлах. Сеть трехфазная. . Исходные данные по вариантам заданы в таблице 2.

Рис. 2

Таблица 2

	А	А	А	Ом	Ом	Ом	Ом
26	50	100	100	1	2	3	2

Данный раздел должен содержать:

• краткие теоретические сведения,

• первую и вторую матрицы инциденций,

• обобщенное уравнение состояния,

• решение матричного уравнения состояния двумя способами (методом обратной матрицы, методом Гаусса),

• решение матричного уравнения состояния методом Крамера в системе MATLAB,

• сравнение полученных промежуточных результатов, найденных разными способами,

• вычисление узловых напряжений аналитически,

• нахождение узловых напряжений с помощью MATLAB- программы,

• сравнение полученных результатов, найденных разными способами.

1.Краткие теоретические сведения

2. первая и вторая матрица инциденций

Первая матрица инциденций без балансирующего узла будет иметь вид:

.

В нашей схеме замещения всего один независимый контур, в соответствии с этим вторая матрица инциденций примет вид:

.

3.Обобщенное уравнение состояния

_{[1,-1,0,0;-1,0,0,-1;0,0,-1,1;-1,-2,3,2]}

4.решение матричного уравнения состояния двумя способами (методом обратной матрицы, методом Гаусса)

1) метод обратной матрицы

_{Находим решение с помощью MATLAB}

_{Обозначим матрицу}

_,

_{а обратную}

_{>> m=[1,-1,0,0;-1,0,0,-1;0,0,-1,1;-1,-2,3,2];}

_{>> minv=inv(m);}

_{>> F=[-50;-100;-100;0];}

_{>> I=minv*F}

_{I =}

_87.5000

_137.5000

_112.5000

_12.5000

_{2) метод Гаусса}

_{Пусть I12=x1;I14=x2;I34=x3;I23=x4;}

_{Тогда запишем систему уравнений}

На главной диагонали, преобразованной матрицы коэффициентов, стоят 1. Теперь проведем преобразования в соответствии с обратным ходом метода Гаусса.

Из последнего уравнения системы определяем . Из предпоследнего уравнения находим . Проведя аналогичные вычисления, получаем

В результате получаем вектор-столбец искомых неизвестных

5.решение матричного уравнения состояния методом Крамера в системе MATLAB

_{>> d=[1,-1,0,0;-1,0,0,-1;0,0,-1,1;-1,-2,3,2];}

_{>> d1=[-50,-1,0,0;-100,0,0,-1;-100,0,-1,1;0,-2,3,2];}

_{>> d2=[1,-50,0,0;-1,-100,0,-1;0,-100,-1,1;-1,0,3,2];}

_{>> d3=[1,-1,-50,0;-1,0,-100,-1;0,0,-100,1;-1,-2,0,2];}

_{>> d4=[1,-1,0,-50;-1,0,0,-100;0,0,-1,-100;-1,-2,3,0];}

_{>> det(d)}

_{ans =}

₈

_{>> det(d1)}

_{ans =}

₇₀₀

_{>> det(d2)}

_{ans =}

₁₁₀₀

_{>> det(d3)}

_{ans =}

₉₀₀

_{>> det(d4)}

_{ans =}

₁₀₀

_{>> x1=det(d1)/det(d)}

_{x1 =}

_87.5000

_{>> x2=det(d2)/det(d)}

_{x2 =}

_137.5000

_{>> x3=det(d3)/det(d)}

_{x3 =}

_112.5000

_{>> x4=det(d4)/det(d)}

_{x4 =}

_12.5000

6.сравнение полученных промежуточных результатов, найденных разными способами

Токи	Методы решения
	Метод обратной матрицы	метод Гаусса	метод Крамера в системе MATLAB
I12	87.5	87.5	87.5
I14	137.5	137.5	137.5
I34	112.5	112.5	112.5
I23	12.5	12.5	12.5

После сравнения мы види, что все токи абсолютно идентичны

7.вычисление узловых напряжений аналитически

По закону Ома определим падение напряжения на ветвях схемы

Используя уравнение , получаем

Перемножая матрицы в матричном уравнении, получаем уравнения с неизвестными, т.е. данная система переопределена. В нашем случае можно выбросить любое уравнение переопределенной системы и решить ее также каким-либо методом решения систем линейных алгебраических уравнений.

8.нахождение узловых напряжений с помощью MATLAB- программы

Вычеркиваем из матрицы M^t последнюю строку и из матрицы U_в аналогично.

>> m=[1,-1,0;-1,0,0;0,0,-1];

>> UB=[87.5;275;337.5];

>> inv(m)*UB

ans =

-275.0000

-362.5000

-337.5000

Отсюда следует, что

9.сравнение полученных результатов, найденных разными способами

Напряжения	Методы решения
	аналитически	С помощьюMATLAB
U1	5725	5725
U2	5637,5	5637,5
U3	5662,5	5662,5