7.2. Эквивалентный генератор
Отключим ветвь с искомым током и рассчитаем эквивалентное напряжение в отсутствии этой ветви (рисунок 7.3):
Рисунок 7.3. Схема для расчёта эквивалентного генератора.
Решим поставленную задачу методом узловых потенциалов:
I U10*Y11+U20*Y12+U30*Y13=J11
II U10*Y21+U20*Y22+U30*Y23=J22
III U10*Y31+U20*Y32+U30*Y33=J33
Где собственные проводимости контуров:
Y11=YС1+YR3= j/4 + 1/8 См
Y22=YR1+YC2=1/4 + j/2 См
Y33=YR3+YC2+(YL2·YR2)/(YL2 + YR2)=1/8 + j/2 + (-j/2·1/4)/(1/4-j/2)=0,325+0,4j См
Взаимные проводимости контуров:
Y13=Y31=-YR3 =-1/8 См
Y12=Y21=0 См
Y23=Y32=-YC2= -j/2 См
Задающие токи узлов:
J11=-J3=1,5j А
J22=- J0 + J2=– 1 + 6 + 3j= 5 + 3j А
J33=J3 - J2=-1,5j – 3j - 6=-6 – 4,5j А
Составим систему уравнений в матричной форме:
Решим полученную систему уравнений в среде MathCAD по формуле U10=|Y1|/|Y|
получим:
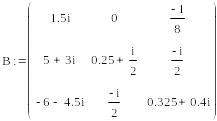
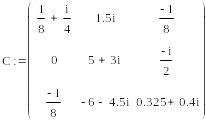
Uэг=Uxx=-0,206 + 11,541j
Приведём эквивалентную модель схемы (рисунок 7.4)
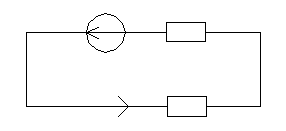
Рисунок 7.4. Схема для нахождения искомого тока I1.
Найдём искомый ток I1. Имеем:
I1=
Итак:
I1=-3,134 + 7,318j – метод контурных токов
I1=-3,134 + 7,318j – метод узловых потенциалов
I1=-3,134 + 7,318j – метод эквивалентного генератора
7.3. Условие выделения максимальной активной мощности в исследуемой ветви
Мощность в исследуемой ветви выделяется максимальная, когда сопротивление Z исследуемой ветви является комплексно-сопряженным с сопротивлением эквивалентного генератора, следовательно, имеем:
для выделения максимальной активной мощности в исследуемой ветви:
Найдём новый ток соответствующий Z=2,036+2,844j Ом
8.Выводы
В данной расчётной работе были рассмотрены методы математического описания и расчёт заданной сложной линейной электрической цепи в стационарном режиме. По методам: контурных токов, узловых напряжений и эквивалентного генератора был найден искомый ток (I1=-3,134 + 7,318j), который получился одинаковым для всех трех методов, что свидетельствует о правильности решения. В работе были проведены исследования цепи на крайних частотах, (Rвх|w=0=16 Ом, Rвх|w→∞=12 Ом) на постоянном токе и при w→∞. Для постоянного воздействии были найдены все токи и проверен баланс мощностей, он оказался верен. Так же в работе были найдены мощность в ветви с искомым током Ps=67,821-34,333j и максимально возможная активная мощность исследуемой ветви Pa=32,762 Вт.
Выполненная работа показала простоту и удобство расчёта цепи различными методами.