
- •Likbez по ТеплоМассоОбмену
- •Раздел 1. Основные понятия теплообмена
- •Раздел 2. Теплопроводность
- •Стационарная теплопроводность в плоской стенке
- •Раздел 3. Конвективный теплообмен в однофазных средах
- •Раздел 4. Конвективный теплообмен при конденсации паров и кипении жидкостей
- •Раздел 5. Теплообмен излучением
- •Раздел 6. Теплопередача через непроницаемые стенки
- •Раздел 7. Теплообменные аппараты
Раздел 6. Теплопередача через непроницаемые стенки
График температурного поля при теплопередаче через плоскую стенку показан на рис. 4. Теплопередача включает в себя следующие процессы: 1) теплоотдачу от горячей текучей среды (горячего теплоносителя) к стенке; 2) теплопроводность внутри стенки; 3) теплоотдачу от стенки к холодной текучей среде (холодному теплоносителю).
Формула для расчета плотности теплового потока через плоскую стенку имеет вид:
![]() ,
,
где![]() – температуры горячего и холодного
флюидов, оС; k –
коэффициент
теплопередачи через плоскую стенку,
Вт/(м2·К).
– температуры горячего и холодного
флюидов, оС; k –
коэффициент
теплопередачи через плоскую стенку,
Вт/(м2·К).
![]() ;
;
где
![]() – коэффициенты теплоотдачи от горячего
флюида к стенке и от стенки к холодному
флюиду, Вт/(м2·К);
– коэффициенты теплоотдачи от горячего
флюида к стенке и от стенки к холодному
флюиду, Вт/(м2·К);
![]() – толщина стенки, м;
– толщина стенки, м;
![]() – коэффициент теплопроводности стенки,
Вт/(м·К);
– коэффициент теплопроводности стенки,
Вт/(м·К);
![]() – термическое сопротивление теплопередачи
через плоскую стенку, (м2·К)/Вт:
– термическое сопротивление теплопередачи
через плоскую стенку, (м2·К)/Вт:
![]() .
.
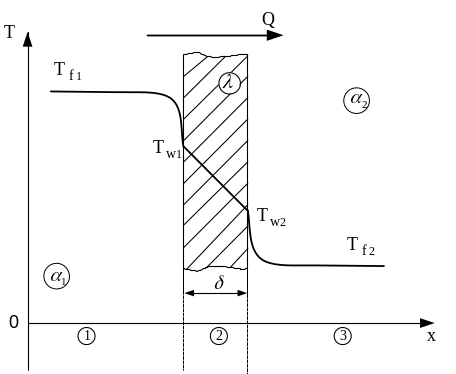
Рис. 4. Теплопередача через плоскую стенку
Термическое сопротивление теплопередачи
через плоскую стенку равно сумме
термического сопротивления теплоотдачи
от горячего флюида к стенке
![]() ,
термического сопротивления теплопроводности
плоской стенки
,
термического сопротивления теплопроводности
плоской стенки
![]() и термического сопротивления теплоотдачи
от стенки к холодному теплоносителю
и термического сопротивления теплоотдачи
от стенки к холодному теплоносителю
![]() .
.
Раздел 7. Теплообменные аппараты
Для теплового расчета рекуперативного теплообменника используют два основных уравнения – уравнение теплового баланса и уравнение теплопередачи. Без учета тепловых потерь в теплообменном аппарате уравнение теплового баланса имеет вид:
![]() ,
,
где
![]() – количество теплоты, отдаваемое горячим
теплоносителем в единицу времени, Вт;
– количество теплоты, отдаваемое горячим
теплоносителем в единицу времени, Вт;
![]() – количество теплоты, воспринимаемое
холодным теплоносителем в единицу
времени, Вт. В развернутом виде уравнение
теплового баланса можно записать:
– количество теплоты, воспринимаемое
холодным теплоносителем в единицу
времени, Вт. В развернутом виде уравнение
теплового баланса можно записать:
а) для однофазных теплоносителей
![]() ;
;
б) при изменении агрегатного состояния горячего теплоносителя (горячий теплоноситель – влажный насыщенный водяной пар)
![]() ,
,
где G1 и G2
– массовые расходы горячего и холодного
теплоносителей, кг/с; cp1
и cp2
– удельные массовые изобарные теплоемкости
горячего и холодного теплоносителей,
Дж/(кгК);
![]() и
и
![]() – температуры горячего теплоносителя
на входе и выходе из теплообменника,
°С;
– температуры горячего теплоносителя
на входе и выходе из теплообменника,
°С;
![]() и
и
![]() – температуры холодного теплоносителя
на входе и выходе из теплообменника,
°С; x – степень сухости
пара.
– температуры холодного теплоносителя
на входе и выходе из теплообменника,
°С; x – степень сухости
пара.
Расходы теплоносителей рассчитывают по уравнению неразрывности:
![]() ,
,
где
![]() – плотность теплоносителя, кг/м3;
– плотность теплоносителя, кг/м3;
![]() – средняя скорость теплоносителя, м/с;
– средняя скорость теплоносителя, м/с;
![]() – площадь поперечного сечения канала
для прохода теплоносителя, м2.
– площадь поперечного сечения канала
для прохода теплоносителя, м2.
Уравнение теплового баланса для однофазных теплоносителей (102) можно записать в виде:
![]() или
или
![]() ,
,
где
![]() и
и
![]()
![]() – расходные теплоемкости (водяные
эквиваленты) горячего и холодного
теплоносителей, Вт/К;
– расходные теплоемкости (водяные
эквиваленты) горячего и холодного
теплоносителей, Вт/К;
![]() и
и
![]() – изменение температур горячего и
холодного теплоносителей в теплообменном
аппарате, °С.
– изменение температур горячего и
холодного теплоносителей в теплообменном
аппарате, °С.
Температуры теплоносителей вдоль поверхности теплообмена изменяются по экспоненциальному закону. При этом из соотношений (111) следует обратно пропорциональная зависимость между водяными эквивалентами и изменениями температуры вдоль поверхности теплообмена (рис. 9):
если
![]() ,
то
,
то
![]() ;
;
если
![]() ,
то
,
то
![]() .
.
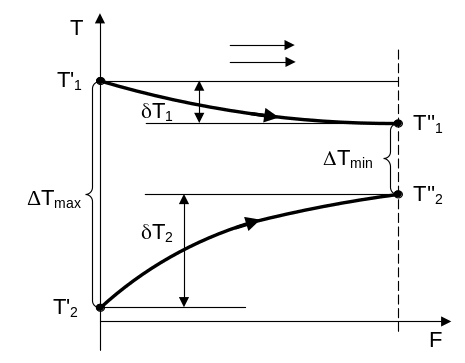
При противоточной схеме движения теплоносителей (рис. 5) выпуклость кривых изменения температуры теплоносителей направлена в сторону большого водяного эквивалента, т.е. в сторону теплоносителя с меньшим изменением температуры.
Если греющим теплоносителем является влажный или сухой насыщенный водяной пар, то в процессе теплопередачи его температура не изменяется и равна температуре насыщения при данном давлении:
![]() .
.
Уравнение теплопередачи в рекуперативном теплообменном аппарате имеет вид:
![]() ,
,
где k – коэффициент
теплопередачи,
Вт/(м2К);
![]() – средняя разность температур между
горячим и холодным теплоносителями
(средний
температурный напор), °С; F
– площадь поверхности теплообмена, м2.
– средняя разность температур между
горячим и холодным теплоносителями
(средний
температурный напор), °С; F
– площадь поверхности теплообмена, м2.
Среднюю разность температур для прямоточной и противоточной схем движения теплоносителей рассчитывают по формулам:
![]() ,
если
,
если
![]()
или
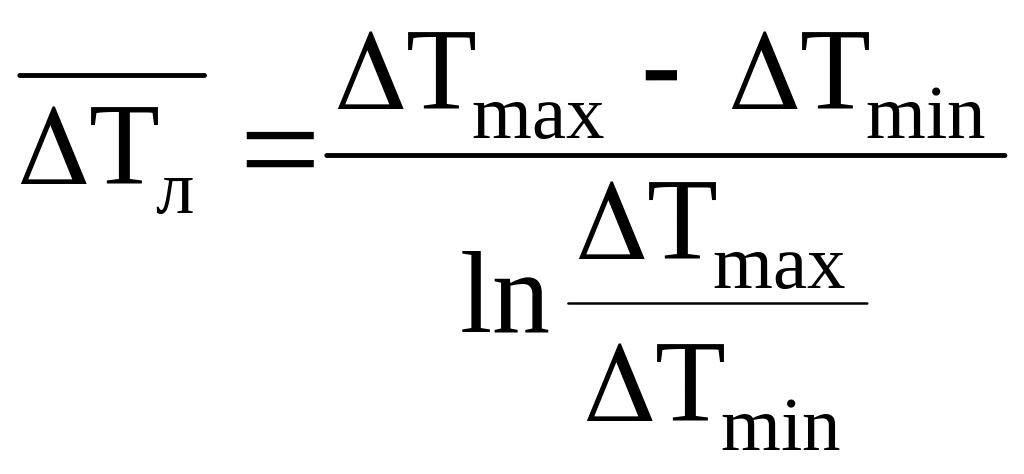 ,
если
,
если
![]() ,
,
где Tmax и Tmin – максимальная и минимальная разности температур теплоносителей (см. рис.9), °С; Tа – среднеарифметическая разность температур, °С; Tл – среднелогарифмическая разность температур, °С.
Для расчета средней разности температур
при сложном движении теплоносителей
строят температурный график
![]() для противотока и
,
рассчитанную по формулам (7.20) или (7.21),
умножают на поправочный коэффициент
для противотока и
,
рассчитанную по формулам (7.20) или (7.21),
умножают на поправочный коэффициент
![]() ,
учитывающий особенности теплообмена
при сложном токе. При этом студент
самостоятельно принимает одну из схем
перекрестного или сложного движения
теплоносителей, приведенных в приложении
[3] и по рисунку определяет
,
учитывающий особенности теплообмена
при сложном токе. При этом студент
самостоятельно принимает одну из схем
перекрестного или сложного движения
теплоносителей, приведенных в приложении
[3] и по рисунку определяет
![]() ,
где комплексы P и R
соответственно равны:
,
где комплексы P и R
соответственно равны:
![]() ;
;
![]() .
.
а) W1>W2 |
|
Рис. 5,а. Изменение температур горячего и холодного теплоносителей вдоль поверхности теплообмена при прямоточной схеме движения в зависимости от соотношения их водяных эквивалентов |
|
|
|
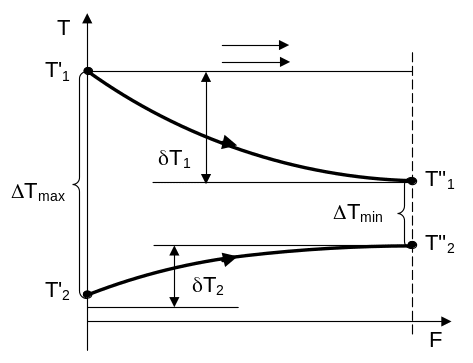
Рис. 5,б. Изменение температуры горячего и холодного теплоносителей вдоль поверхности теплообмена при противоточной схеме движения в зависимости от соотношения их водяных эквивалентов |
|
Профессор кафедры ТОТ, д.т.н. Бухмиров В.В.
Январь, 2007 г.

 б)
W1<W2
б)
W1<W2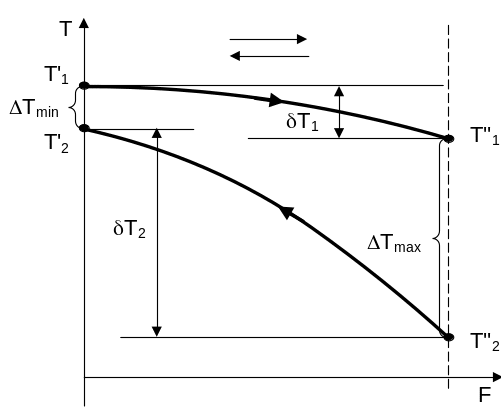 а) W1>W2
а) W1>W2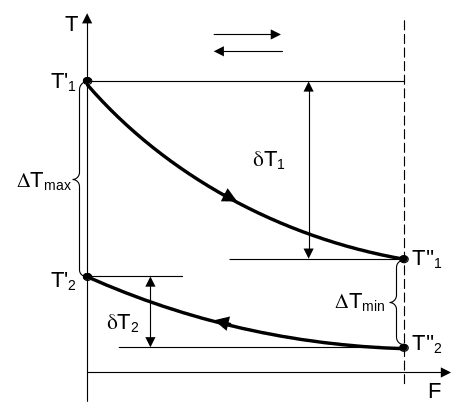 б) W1<W2
б) W1<W2