3.1.2 Несиметричне навантаження фаз споживача, з’єднаних зіркою

У випадку несиметричного навантаження фаз споживача (Z_A ¹ Z_B ¹ Z_C) використовують чотирипровідне трифазне коло.

Приклад 2. Фазна напруга споживачів у чотирипровідному трифазному колі В. Комплексні опори кожної із фаз споживача становлять:

Ом; Ом; Ом.

Визначити струм у нейтральному проводі та побудувати векторну діаграму напруг і струмів.

Розв´язок

Приймемо, що вектор фазної напруги співпадає з віссю дійсних чисел. Тоді

Струм в нейтральному проводі

Рисунок 3.3 – Векторна діаграма напруг і

струмів трифазного несиметричного споживача, з’єднаного зіркою

Векторна діаграма струмів та напруг для цього випадку побудована на рисунку3.3.

Нейтральний провід вирівнює потенціали нейтральних точок джерела та споживача. За рахунок цього забезпечується рівність діючих значень фазних напруг споживача

.

У трифазному колі при несиметричному навантаженні фаз та відсутності нейтрального проводу напруги на фазах споживача не будуть рівні між собою (U_A ¹ U_B ¹ U_C) тому, що між нейтральними точками джерела та споживача виникає напруга . Ця напруга називається напругою зміщення нейтралі.

Напругу зміщення нейтралі визначають в комплексному вигляді за формулою:

де Y_A, Y_B, Y_C та Y_N – комплексні провідності фаз та нейтрального проводу.

При відсутності нейтрального проводу напруга для даного прикладу дорівнює:

Струми у фазах навантаження

Згідно з першим законом Кірхгофа

Векторна діаграма для трифазного кола при з’єднанні зіркою без нейтрального проводу побудована на рисунку 3.4.

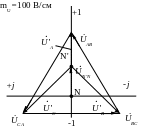
Рисунок 3.4 – Векторна діаграма напруг трифазного несиметричного споживача, з’єднаного зіркою, при відсутності нейтрального проводу

На векторній діаграмі (рисунок 3.4) - комплексні напруги на фазах споживача.

3.2 Розрахунок електричних кіл при з’єднанні фаз споживачів трикутником

С

.

хема з’єднання фаз споживачів електроенергії трикутником, зображена на рисунку 3.5.

Рисунок 3.5 – Схема трифазного кола при з’єднанні фаз споживача трикутником

Струми в лінійних проводах , , називають лінійними. Струми , , , що протікають через фази споживачів називаються фазними.

При симетричному навантаженні (Z_АВ= Z_ВС = Z_СА) фазні та лінійні струми і напруги визначають:

,

а при несиметричному навантаженні (Z_АВ ¹ Z_ВС ¹ Z_СА), , лінійні струми визначають за першим законом Кірхгофа:

3.2.1 Симетричне активне навантаження

Приклад 3. Навантаження фаз Z_АВ = Z_ВС = Z_СА = R = 22 Ом; U_Л = 220 В. Визначити лінійні та фазні струми, побудувати векторну діаграму напруг і струмів при з’єднанні фаз трикутником.

Приймаємо, що вектор напруги співпадає з додатнім напрямом осі дійсних чисел комплексної площини.

Тоді струми у фазах

Згідно з першим законом Кірхгофа струми в лінійних проводах

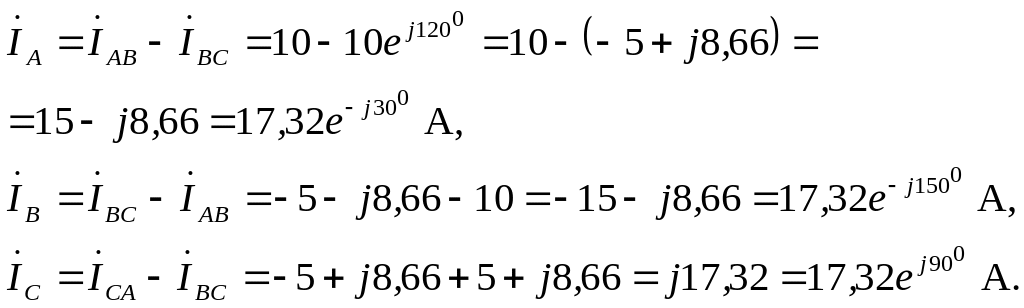
Векторна діаграма для даного випадку побудована на рисунку 3.6.

Рисунок 3.6 – Векторна діаграма напруг і струмів для симетричного споживача, з’єднаного трикутником