6. Алгебра Жегалкіна

Розглянемо окремо одну важливу систему твірних для алгебри булевих функцій <P₂,{S}>, а саме систему ₅ = {,,1}. Функціональна повнота системи ₅ була обгрунтована в прикладі 6.1(3) методом зведення.

Поруч із класичною алгеброю логіки C = <B,{,,^—}>, введеною у розділі 4, значне місце у теорії булевих функцій займає алгебра G = <B,{,,1}> із сигнатурою ₅. Ця алгебра дістала назву алгебри Жегалкіна, на честь математика І.І.Жегалкіна, який запропонував алгебру G і дослідив її основні властивості.

Як і для алгебри C, подамо основні тотожності алгебри Жегалкіна. Відзначимо тільки властивості операції  та її зв’язок з іншими операціями алгебри G. Усі тотожності з (6.3) відносно операцій  і 1 справедливі, очевидно, і в алгебрі G.

1. (xy)z = x(yz) (асоціативність),

2. xy = yx (комутативність),

3. x(yz) = xyxz (дистрибутивність),

4. xx = 0, x0 = x,

5. x1 =  .

Зауважимо, що в алгебрі Жегалкіна введено порядок виконання операцій: спочатку виконуються кон’юнкції, потім - додавання за модулем 2.

Із повноти системи ₅ випливає, що будь-яка булева функція f(x₁,x₂,...,x_n) може бути реалізована деякою формулою над ₅, тобто формулою в алгебрі Жегалкіна. Якщо в цій формулі розкрити всі дужки за законом дистрибутивності, а потім здійснити всі спрощення за допомогою основних тотожностей алгебри G, то одержимо рівносильну формулу, яка зображує функцію f і має вигляд

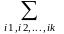a_i1i2...ikx_i1x_i2...x_ik, a_i1i2...ikB; 0  k  n (6.10)

Тут  є знаком додавання за модулем 2, усі доданки попарно різні, у кожній кон’юнкції жодна змінна не зустрічається більше одного разу. Деякі доданки можуть містити тільки одну змінну (k = 1) - це лінійні доданки. Нарешті, можливий єдиний доданок з порожньою кон’юнкцією змінних (k = 0), яка вважається рівною 1; відповідний коефіцієнт a₀ є вільним членом формули.

Формула (6.10) називається поліномом Жегалкіна булевої функції f(x₁,x₂,...,x_n). Множники a_i1i2...ik називають коефіцієнтами полінома Жегалкіна. Кількість доданків у поліномі Жегалкіна називають його довжиною, а найбільший ранг його елементарної кон’юнкції - степенем цього полінома.

7. Критерій Поста — одна з центральних теорем математичної логіки, описує необхідні та достатні умови функціональної повноти множини булевих функцій. Був сформульований американським математиком Емілем Постом в 1941. Отже, для того щоб наша система була повною, необхідно і достатньо, щоб вона містила хоча б одну нелінійну функцію, хоча б одну несамодвоїсту, хоча б одну немонотонну, хоча б одну функцію, яка не зберігатиме нуль та хоча б одну функцію, що не зберігає одиницю.

Існує п`ять найважливіших замкнених класів:

клас   функцій, що зберігає 0;

клас   функцій, що зберігає 1;

клас   самодвійкових функцій;

клас   монотонних функцій;

клас   лінійних функцій.

За́мкнений клас фу́нкцій а́лгебри ло́гіки — така множина P функцій алгебри логіки, замикання якої відносно операції суперпозиції збігається з ним самим, тобто [P] = P.

Тобто, довільна функція, яку можна представити формулою з використанням функцій множини P, також входить в цю множину:

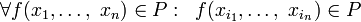•  (замкнутість щодо заміни змінних);

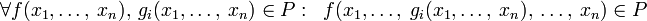•  (замкнутість щодо суперпозиції).

Замкненим класом функцій алгебри логіки є, наприклад, клас   всіх функцій алгебри логіки.

В 1941 році Еміль Пост надав повний опис замкнених класів, який назвали решіткою Поста.