1. Елементарні булеві функції

У теорії булевих функцій особливе місце займають функції однієї змінної - унарні (n = 1) і функції двох змінних - бінарні (n = 2), про які йтиметься нижче.

Існує 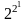 = 4 різних булевих функцій від однієї змінної (унарних булевих функцій або унарних булевих операцій).

Функції ₀ і ₃ - це константи 0 і 1; значення цих функцій не залежать від значень змінної x і тому змінна x є несуттєвою. Функція ₁ "повторює" значення аргумента x, ₁(x) = x, і називається тотожною функцією. Єдиною нетривіальною функцією є функція ₂(x). Будемо називати цю функцію функцією заперечення змінної x і позначати через 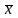, тобто ₂(x) =  . Іноді функцію ₂(x) називають також інверсією, або функцією НІ, і позначають через ¬x або x'.

Кількість булевих функцій від двох змінних (бінарних булевих функцій або бінарних булевих операцій) згідно з теоремою 6.1 дорівнює  = 2⁴ = 16.

Із 16 булевих функцій від двох змінних 6 функцій мають фіктивні змінні і зводяться до функцій від меншого числа змінних. Функції ₀ і ₁₅ є константами 0 і 1 відповідно, тобто є функціями, обидві змінні яких є несуттєвими. Функції ₃ і ₅ "повторюють" одну зі своїх змінних: ₃(x,y) = x і ₅(x,y) = y, а функції ₁₀ і ₁₂ є запереченнями одної зі своїх змінних: ₁₂(x,y) =  і ₁₀(x,y) =  .

Решта 10 функцій суттєво залежать від обох своїх змінних. Для цих функцій використовують спеціальні назви і позначення за допомогою певних знаків бінарних операцій.

Функція ₁(x,y) називається кон’юнкцією (логічним множенням, функцією збігу або логічним І) x і y і позначається xy, x&y, min(x,y) або xy (за аналогією зі звичайним числовим множенням знак кон’юнкції часто випускають і записують xy).

Функція ₇(x,y) називається диз’юнкцією (логічним додаванням, з’єднувальним або логічним АБО) x і y і позначається xy, max(x,y) або x+y.

Функція ₆(x,y) - це додавання за модулем 2. Її позначають xy, xy або xy. Функція ₆ набуває значення 1, коли значення її аргументів різні, і значення 0, коли вони збігаються. Тому функцію ₆ також називають функцією нерівнозначності, альтернативою або розділовим АБО.

Функцію ₉(x,y) називають функцією еквівалентності або рівнозначності і позначають x~y, xy або xy. Вона дорівнює 1, коли значення її аргументів рівні між собою, і дорівнює 0, коли вони різні.

Функція ₁₃(x,y) носить назву імплікації і позначається xy або x  y. Ці позначення читаються “якщо x, то y” (“з x випливає y” або “x імплікує y”) звідки ще одна назва цієї функції - логічне слідування.

Функцію ₁₄(x,y) називають штрихом Шеффера (антикон’юнкцією або функцією НІ-І), позначають x|y; а функцію ₈(x,y) - стрілкою Пірса (антидиз’юнкцією, функцією НІ-АБО, функцією Даггера або функцією Вебба), позначають xy.

Інші функції: ₂ - антиімплікація (-/    ), ₄ - зворотна антиімплікація (/-    ) i ₁₁ - зворотна імплікація () використовуються рідше, ніж вищезгадані.

Булеві константи 0 і 1 можна розглядати як виділені (фіксовані) елементи, тобто як нульарні операції алгебри логіки, або нульарні булеві функції.

Усі невироджені булеві функції від одної і двох змінних (унарні і бінарні булеві функції), а також нульарні булеві функції назвемо елементарними булевими функціями.

Нижче буде доведено, що з елементарних булевих функцій за допомогою операції суперпозиції S можуть бути одержані всі булеві функції, тобто множина елементарних булевих функцій є системою твірних для алгебри <P₂,{S}>.

2. Тео́рія множи́н — розділ математики, в якому вивчаються загальні властивості множин (переважно нескінченних). Виділення теорії множин в самостійний розділ математики відбулося на рубежі XIX і XX століть. Теорія множин зробила дуже великий вплив на розвиток сучасної математики — вона являється фундаментом ряду нових розділів математики, дозволила по-новому поглянути на класичні розділи математики і глибше зрозуміти сам предмет математики.

Сучасні дослідження теорії множин була започатковані Георгом Кантор і Ріхардом Дедекіндом в 1870-х роках. Після відкриття парадоксівнаївної теорії множин, на початку ХХ століття були запропоновані численні системи аксіом, серед яких найвідомішою є система Цермело-Френкеля, з аксіомою вибору.

В основі теорії множин лежать первинні поняття: множина та елемент множини. Елемент множини перебуває щодо множини у відношенні бути елементом множини (позначається як  ^[4] — «x є елемент множини A»). Серед похідних понять найважливішими є наступні:

• порожня множина — множина, яка не містить елементів, позначається зазвичай  ;

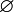• підмножина і надмножина — множина, яка складається тільки з елементів іншої множини, та множина, до якої належать усі елементи іншої множини, відповідно;

• сімейство множин;

• простір (універсум) — множина, що є надмножиною всіх множин;

• конституента.

Над множинами визначені наступні операції:

• об'єднання (або сума) (позначається як  );

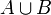• перетин (або добуток) (позначається як  );

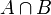• різниця (позначається як 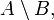  рідше  );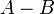

• симетрична різниця (позначається як 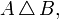  рідше  ).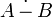

• доповнення (позначається як 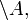  або  );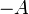

Для множин визначені наступні бінарні відношення:

• відношення рівності (позначається як  );

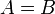• відношення включення (позначається як 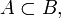  або 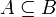 ).