2.4.Статистичні дослідження впливу факторів на дослідження.

З’ясуємо залежність між обсягом продукції та обсягом реалізація продукції молока.

Таблиця.2.5

Розрахункові показники для складання системи нормативних рівнянь.

Роки	Обсяг продукції молока та молочної продукції (тис.т)	Обсяг реалізації молока та молочної продукції (тис.т.)	Розрахункові величини
n	x	y	х2	у2	ху	ух
2005	2.4	2121.3	5.76	4499913.6	5091.12	2079.26
2006	1.7	2017.3	2.89	4069499.2	3429.41	2026.41
2007	1.0	1824.8	1.0	3329895	1824.8	1973.56
2008	0.6	1834.3	0.36	3364656.4	1100.58	1943.36
2009	0.7	1993.9	0.49	3975637.2	1395.73	1950.91
2010	0.7	2004.1	0.49	4016416.8	1402.87	1950.91
2011	0.5	2061.3	0.25	4248957.6	1030.65	1935.81
Всього	7.6	13857	11.24	27504974	15275.16	13860
В серед.	1.08	1979.6	1.6	3929282	2182.16	1980

Використовуючи дані таблиці, розрахуємо коефіцієнти регресії:

у_х =а₀ +а₁х

∑y =na₀ + a₁∑x

∑xy =a₀∑x + a₁∑x²

13857=7a₀+7.6а₁

15275.16=7.6а₀+11.24а₁

Поділимо кожне рівняння на коефіцієнт при а₀

1979.6=а₀+1.08а₁

2009.8=а₀+1.48а₁

Віднімемо від другого рівняння перше та знайдемо значення параметра а₁:

30.2=0.4а₁

а₁=75.5

Підставимо значння параметра а₁ в рівняння і знайдемо а₀:

2009.8= а₀+111.74

а₀=1898.06

Підставимо знайдені параметри у рівняння прямої:

Y_x = 1898.06 –75.5x

Для побудови графіку, знайдемо вирівняні значення, підставивши отримані параметри у рівняння.

У 2005 році ху =1898.06 –75.5*2.4=2079.26

2006 році ху=1898.06 –75.5*1.7=2026.41

2007 році ху =1898.06 –75.5*1.0=1973.56

2008 році ху=1898.06 –75.5*0.6=1943.36

2009 році ху =1898.06 –75.5*0.7=1950.91

2011 році ху=1898.06 –75.5*0.5=1935.81

Для оцінки щільності зв’язку зазначених ознак розрахуємо лінійний коефіцієнт парної кореляції.

r = (XY – X * Y) / (_{x *} _y) , де

_x =  Х² – (Х)² , _у =  Y ² – (Y)²

_x =  1.6 – 1.08² =  1.6 – 1.1664 = 0.6

_у =  3929282 – 1979.6² = 102

r = (2182.16 – 1.08 * 1979.6) / (0.6 * 102) = 44.19 / 61.2 =0.722

Розрахункові значення лінійного коефіцієнта парної кореляції вказує на те що між данними колелюючими ознаками існує прямий тісний зв’язок , оскільки значення коефіцієнта знаходиться в межах 0.7≤r≤0.999 з метою визначення % впливу обраного факторного чинника . Розраховуємо коефіцієнт детермінації:

D = r²*100%

Так D =(0.722)² *100%= 52.13 % (47.87%)

З метою перевірки вирогідності зв’язку визначемо значення t-критерієм Ст’юдента.

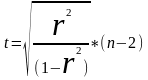
t=5.49

Оскільки значення t більше за табличний (t= 2.447)відкидається гіпотеза про випадковість виявленного зв’язку між корелюючи ми ознаками.

Зобраземо виявлену модель графічно.

Рис. Кореляційна залежність між обсягом продукції та обсягом реалізації молока та молочної продукції.

Оскільки точки імперичного полю регресії не суттево віддалені від лінії регресії виявлений зв’язок ( щільний) вважається підтвердженим.

Таблиця.2.6

Визначення залежності між реалізацією та виробництва молока та молочної продукції.

Роки	Реалізація продукції тис.т	Виробництво продукції тис.т	Розрахункові величини
			Rx	Ry	d	d2
2005	2121.3	32.7	1	4	-4	16
2006	2017.3	48.7	2	7	-5	25
2007	1824.8	45.5	3	6	-3	9
2008	1834.3	28.7	4	3	1	1
2009	1993.9	39.7	5	5	0	0
2010	2004.1	19.3	6	2	4	16
2011	2061.3	14.8	7	1	6	36
Всього	13857	229.4				103

Рангування проводиться за кожною із ознак окремо :

1. Найменшому -1ранг; останній – найбільший

2. Щільність зв’язку визначається на підставі коефіцієнта Спірмена:

R=1-

R=1- =0.84

D=R²*100%=70.56%(29.44%)

РОЗДІЛ 3. ШЛЯХИ ВИЗНАЧЕННЯ РЕЗУЛЬТАТІВ.