5. Расчет переходного процесса регулируемого параметра в сау.

На рис. 4 представлена структурная схема САУ в программе МВТУ для расчета переходного прочеса по каналу управляющего воздействия.

Р ис. 4 структурная схема сау в программе мвту для расчета переходного прочеса по каналу управляющего воздействия.

На рис. 5 представлена кривая в программе МВТУ переходного процесса.

Р ис. 5 кривая в программе мвту переходного процесса.

6. Определение показателей качества регулирования и максимального регулируемого параметра.

Построим кривую переходного процесса.

Для этого найдём переходную функцию h(t) через обратное преобразование Лапласа.

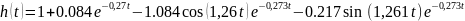
По кривой представленной на рис. 5 определим время регулирования.

Д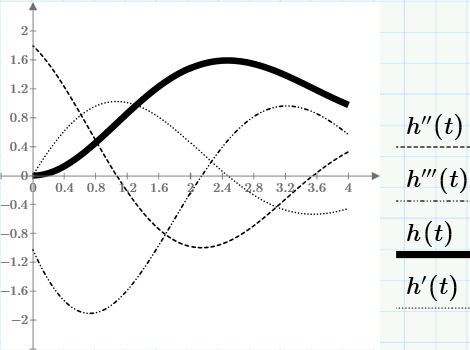 ля этого на кривой отмечаем от , и проводим линии параллельные оси абцис. На пересечении кривой и нижней линии получаем точку это и есть время регулирования .

Перерегулирование рассчитывается по формуле:

t,c

Рис.6 Участок кривой переходного процесса и её производных.

Определяем максимальное ускорение . Для этого найдём максимум функции ,

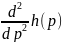Максимум функции находится в точке , следовательно w₀=1.8.

7. Определение показателей качества регулирования.

Показатели качества регулирования вычисляются по следующим формулам: . Получим:

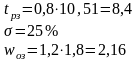
8. Построение лачх не изменяемой части разомкнутой сау.

Возьмем передаточную функцию разомкнутой САУ формула (13)

Подставив значения передаточных функций получим:

Найдем сопряженные частоты:

На рис.6 представлена ЛАЧХ не изменяемой части разомкнутой САУ.

9. Построение желаемой лачх

Для построения желаемой ЛАЧХ , найдем частоту среза 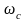, для среднечастотной асимптоты. Для этого используем номограмму, составленная В.В. Солодниковым на рис. 8. По заданному значению перерегулирования определим отношение между . Используя формулу :

. (1.7)

Дано , от сюда получаем , тем самым мы нашли частоту при которой время регулирования не превысит заданного значения. При начальном рассогласовании ускорение регулируемой величины ограничивается значением , то максимальное значение определяется из отношения:

, (1.8) где . Получим:

Т.к. 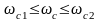, то частоту среза принимаем

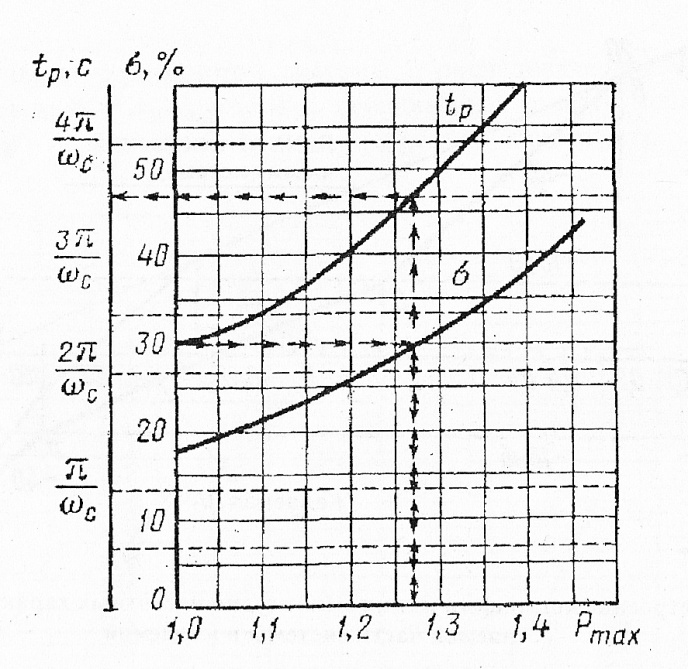
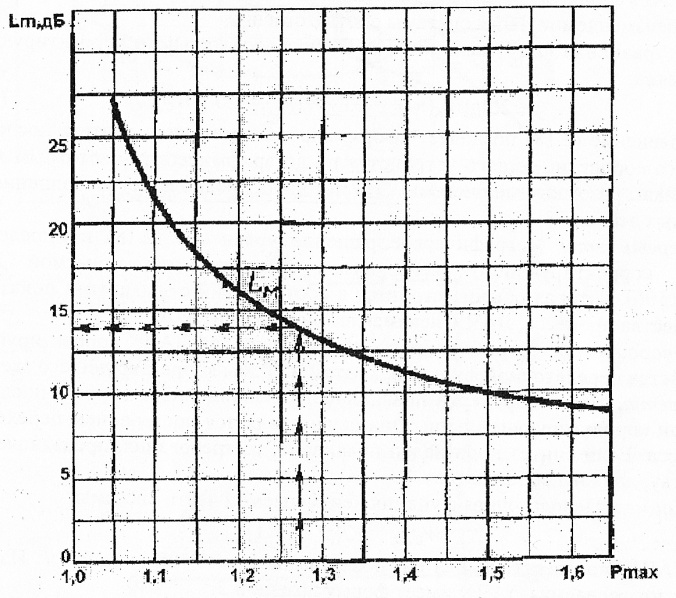
Рис. 9 Зависимость значений желаемой ЛАЧХ на границах среднего поддиапазона от максимума вещественной частотной характеристики разомкнутой системы.

системы.

Рис.8 Показатели качества регулирования САУ в зависимости от максимума вещественной частотной характеристики разомкнутой системы.

Средне частотная асимптота желаемой ЛАЧХ проводится через частоту среза с наклоном -20 дБ/дек.

Найдем частоту сопряжения с низкочастотной областью. Для этого воспользуемся номограммой на рис. 9, по ней определяем предельные значения логарифмических амплитуд. В нашем случае это значение 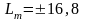. На этих отметках проводим линии параллельные оси частот. В точках пересечения этих линий и средне частотной асимптоты мы получаем сопрягающие частоты. Для определения низкочастотной области воспользуемся следующим выражением

Возьмем ω=1 получим:

Возьмем ω=К получим:

По этим 2 тучкам строем наклонную линию АВ, её наклон -20дБ/дек.

Из точки сопряжения низкочастотной и средне частотной проводим наклонную, с наклоном -40дБ/дек, до пересечения с линией АВ.

Высоко частотную асимптоту проводим параллельно желаемой ЛАЧХ, т.к. она мало влияет на свойства системы.

На рис.7 представлена желаемая ЛАЧХ .

­

10. Определение ЛАЧХ корректирующего звена.

Т.к в нашей системе корректирующее звено последовательное, то для построения ЛАЧХ корректирующего звена, воспользуемся формулой:

(1.9).

На рис.7 представлена ЛАЧХ корректирующего звена.

11. Определение передаточной функции разомкнутой САУ по желаемой ЛАЧХ .

Для определения передаточной функции разомкнутой САУ по желаемой ЛАЧХ воспользуемся рис.7. Получим:

Исходя из того что низкочастотный участок желаемой ЛАЧХ совпадает с неизменяемой ЛАЧХ, следовательно К=33,75.

Найдем частоты сопряжения и получим Т

По ЛАЧХ Подставим найденные Т, получим

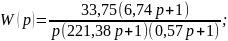
12. Определение передаточной функции корректирующего звена по ЛАЧХ .

Для определения передаточной функции разомкнутой САУ корректирующего звена по полученной ЛАЧХ воспользуемся рис.7. Получим:

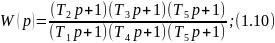
Найдем частоты сопряжения и получим Т

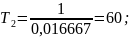
По ЛАЧХ Подставим найденные Т, получим

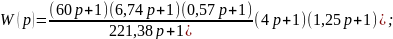
3. Расчет переходного процесса скорректированной САУ.

На рис. 9 представлена структурная схема скорректированной САУ в программе МВТУ для расчета переходного прочеса по каналу управляющего воздействия.

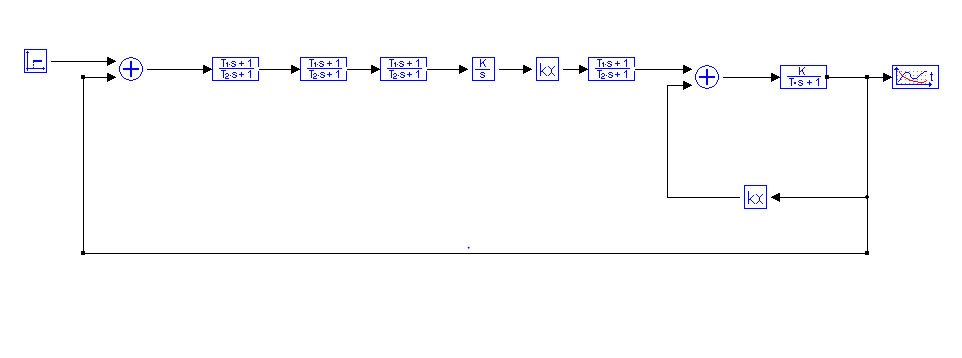
рис. 9 структурная схема скорректированной САУ в программе МВТУ для расчета переходного прочеса по каналу управляющего воздействия.

На рис. 10 представлена кривая в программе МВТУ переходного процесса.

14. Определение запаса устойчивости скорректированной САУ по амплитуде и фазе.

Для определения запаса устойчивости по фазе из точки пересечения ЛАЧХ с осью частот опускается вертикаль до угла -180, при этом отрезок между кривой ЛФЧХ и уровнем -180 даст величину запаса устойчивости.

Для определения запаса устойчивости по амплитуде, необходимо восстановить вертикаль из точки пересечения ЛФЧХ с линией -180 до пересечения с осью частот. При этом отрезок между графиком ЛАЧХ и осью абсцисс даст нам величину запаса по амплитуде.

Из выражения , запишем ФЧХ:

Значения ФЧХ при разных ω представлены в таблице 4.

Таблица 4

Ω	0	0,001	0,005	0,01	0,05	0,1	0,5	1
φ(ω)	-90	-123,7	-156	-156,3	-124	-109	-94	-91,6

На рис.11 показано нахождение запаса устойчивости по фазе и амплитуде.

.

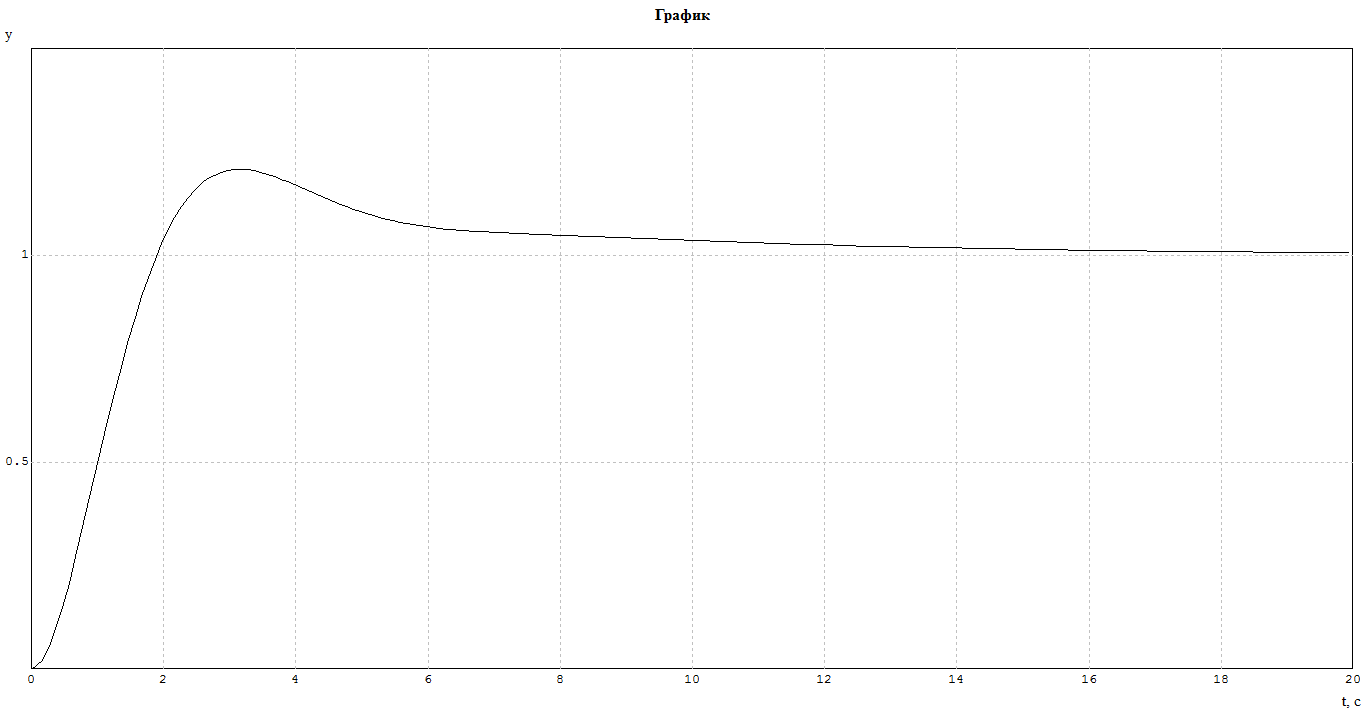
рис. 10 кривая в программе МВТУ переходного процесса.