Задача 4

На предприятии в порядке случайной выборки получили следующие данные о выполнении норм выработки:

% выполнения норм выработки	до 100	100-110	110-120	120-150	Всего
Число рабочих	44	408	70	28	550

На основании приведенных данных определить:

а) удельный вес рабочих, выполняющих и перевыполняющих нормы выработки;

б) среднюю ошибку выборки для доли и предельную ошибку для бесповторного отбора с вероятностью 0,9876. Общая численность рабочих 3700 человек.

Решение:

а) Удельный вес рабочих, выполняющих и перевыполняющих нормы выработки, определим по формуле:

Уд. вес = число рабочих / всего рабочих * 100%

До 100: уд.вес = 44/550*100% = 8%

100 - 110: уд.вес = 408/550*100% = 74,2%

110 - 120: уд.вес = 70/550*100% = 12,7%

120 - 150: уд.вес = 28/550*100% = 5,1%

б) Средняя ошибка выборки для доли:

, где

w – доля единиц в выборочной совокупности; w = m/n, где m – число единиц, обладающих изучаемым признаком, n – число выборки.

N – объём генеральной совокупности;

n – объём выборочной совокупности.

Предельная ошибка для доли:

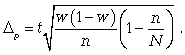
t - коэффициент кратности (при вероятности 0,9876 t=2,5)

N = 3700

n = 550

До 100:

w = 0,08

µ_с = √0,08*(1-0,08)*(1-550/3700) = √0,0736*0,85 = √0,06256 = 0,25

Д_с = 2,5 * 0,25 = 0,625

100 - 110:

w = 0,742

µ_с = √0,742*(1-0,742)*(1-550/3700) = √0,19*0,85 = √0,1615= 0,4

Д_с = 2,5 * 0,4 = 1

110 - 120:

w = 0,127

µ_с = √0,127*(1-0,127)*(1-550/3700) = √0,11*0,85 = √0,0935 = 0,31

Д_с = 2,5 * 0,31 = 0,78

120 - 150:

w = 0,051

µ_с = √0,051* (1-0,051)*(1-550/3700) = √0,0484*0,85 = √0,04114 = 0,2

Д_с = 2,5 * 0,2 = 0,5

Составим результирующую таблицу:

% выполнения норм выработки	до 100	100-110	110-120	120-150	Всего
Число рабочих	44	408	70	28	550
Удельный вес, %	8	74,2	12,7	5,1	100
Средняя ошибка выборки	0,2	0,4	0,31	0,2	-
Предельная ошибка	0,625	1	0,78	0,5	-

Задача 5

Рассчитайте дисперсию и среднее квадратичное отклонение методом отсчета от условного нуля.

Г одовой удой молока, л	Число коров (f)	Середина интервала (x)	x – A ¾¾ k	x – A ¾¾ f k	x – A 2 ¾¾ f k
До 1000	2
1000-2000	8
2000-3000	23
3000-4000	13
4000-5000	2
Итого	48

Решение:

Примем А = 2500 – интервал, имеющий наибольшую частоту; k = 1000.

Г одовой удой молока, л	Число коров (f)	Середина интервала (x)	x – A ¾¾ k	x – A ¾¾ f k	x – A 2 ¾¾ f k
До 1000	2	500	-2	-4	8
1000-2000	8	1500	-1	-8	8
2000-3000	23	2500	0	0	0
3000-4000	13	3500	1	13	13
4000-5000	2	4500	2	4	8
Итого	48			5	37

Дисперсия рассчитывается по формуле:

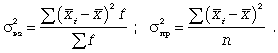
у² = 37/48 = 0,77

Среднее квадратичное отклонение:

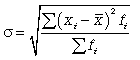
у = √0,77 = 0,88

При расчете методом отсчета от условного нуля полученные значения умножаем на k:

у² = у² * k = 0,77*1000 = 770 (л)

у = у * k = 0,88 * 1000 = 880 (л)

Ответ: дисперсия равна 770 л; среднее квадратичное отклонение составит 880 л.