§8 Производная сложной функции.

Пусть , . Тогда – сложная функция, где u – промежуточный аргумент, x – независимая переменная. Требуется найти производную сложной функции.

Теорема: Если функция имеет в т. x производную , а функция имеет при соответствующем значении u производную , то сложная функция в точке x имеет производную, равную

(или ).

Без доказательства.

Итак: Производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

§9 Производные степенной и показательной функций.

1. Производная степенной функции y=xⁿ,

Пример. .

2) Производная показательной функции y=a^x, a>0,

Прологарифмируем обе части по основанию e

,

Продифференцируем обе части по x

Частный случай

Примеры:

1. 2)

§10. Производная обратной функции. Производные обратных тригонометрических функций. Производная логарифмической функции.

1. Производная обратной функции.

Теорема: Пусть функция монотонна и дифференцируема в некотором интервале и имеет в т. y этого интервала . Тогда в соответствующей точке x обратная функция имеет производную , причем или .

Без доказательства.

2. Производные обратных тригонометрических функций.

1. Производная функции y=arcsin x.

Рассмотрим функцию , где , . Эта функция возрастает, непрерывна, дифференцируема существует обратная функция , где ; . Существует и производная этой функции, равная .

Замечание. Исключили x=±1, (y=±π/2), т.к. иначе

2. Производная функции y=arccos x.

3. Производная функции y=arctg x.

Рассмотрим функцию , где , . Эта функция возрастает, непрерывна, дифференцируема существует обратная функция , ; и существует производная этой функции, равная .

4. Производная функции y=arcсtg x. (вывести самостоятельно)

3. Производная логарифмической функции y=log_ax; a>0, a≠1

Вывести самостоятельно тремя способами:

1-способ – по определению

2-способ – использую производную обратной функции

3-способ – логарифмированием обеих частей.

§11. Таблица основных производных и правила дифференцирования.

Таблица производных.

1. 5.

2. 6.

7.

8.

9.

3. 10.

11.

4. 12.

Основные правила дифференцирования.

5. , :

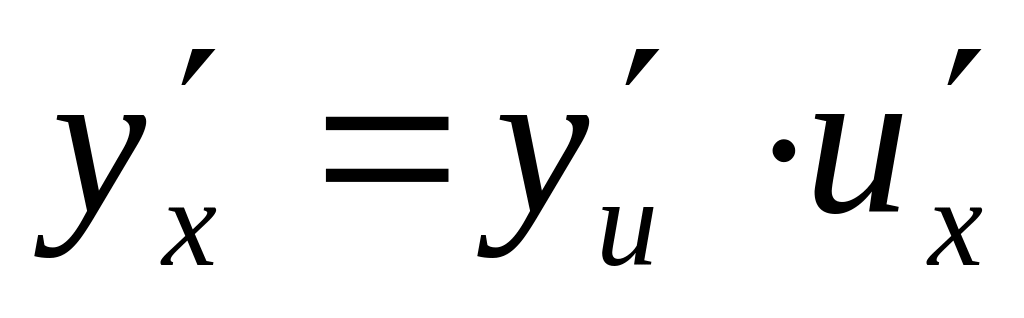
Примеры:

1. 

2. 

3. 

4. 

5. 

Замечание. Дифференцирование показательно-степенной функции.

Пусть , где ,

Прологарифмируем по основанию е:

Продифференцируем по х:

Умножим на :