12. Цифровые методы анализа: оценивание кореляционных функций методом бпф, оценки спектральной плотности мощности и алгоритмы вычисления

Для определения оценок спектральной плотности мощности используют корреляционный метод, основанный на использовании соотношения

(12.1)

То есть в начале с использованием (12.1) рассчитывалась оценка ковариационной функции, а затем оценка спектральной плотности мощности вычислялась как преобразование Фурье при соответствующем значении максимального сдвига.

Рис. 12.1.

Исходная оценка функции ковариации вводится в ЗУ, с помощью которого она периодически воспроизводится и анализируется затем на заданных частотах с помощью соотношения (12.1). Синхронизация воспроизведения функции с фазой выходных колебаний генератора производится с помощью блока управления и получаемые значения СПМ фиксируются в устройстве регистрации.

Разобьём реализацию на смежных отрезков длиной T каждый и обозначим эти отрезки через :

Тогда оценка спектральной плотности мощности на произвольной частоте f может быть записана как:

(12.2)

где

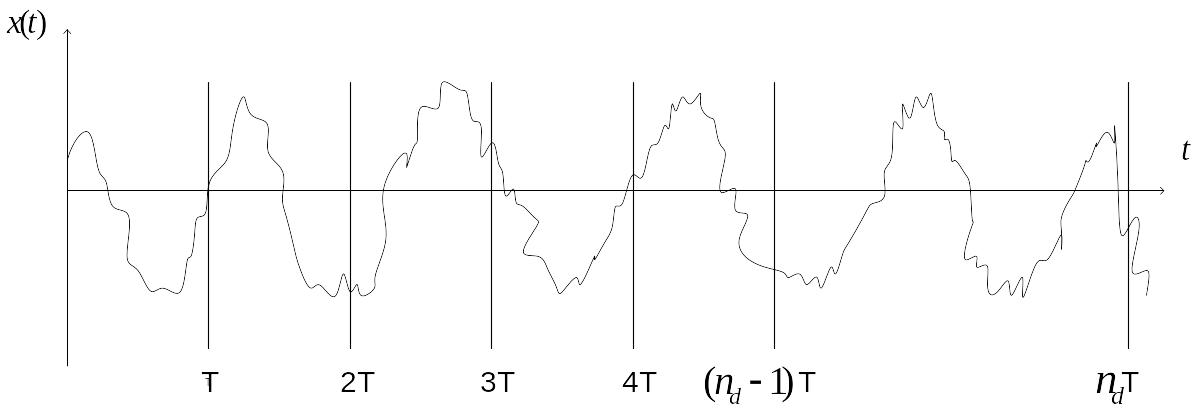
Рис. 12.2

При дискретном временном параметре каждая реализация будет представлена N значениями временного ряда 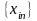, . Конечное преобразование Фурье даст соответствующее соотношению (12.2) значения спектральной плотности мощности на дискретных частотах

При этом коэффициенты Фурье для каждого отрезка определяются как

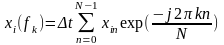(12.3)

При этом оценка двусторонней спектральной плотности принимает вид

(12.4)

В свою очередь, односторонняя функция СПМ оценивается как:

(12.5)

Число отсчётов N в соотношении для СПМ при каждом БПФ называют размером блока и оно служит ключевым параметром, определяющим разрешающую способность по частоте

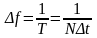
Кроме того, при осуществлении БПФ по алгоритму Кули – Тьюки размер выборки удобно выбирать как целую степень числа 2, т.е. .

Определённое формулой (12.3) конечное преобразование Фурье функции можно рассматривать как преобразование Фурье заданной на бесконечном интервале функции , умноженной на прямоугольное «временное окно» , имеющее вид:

Иными словами реализацию можно рассматривать как произведение .

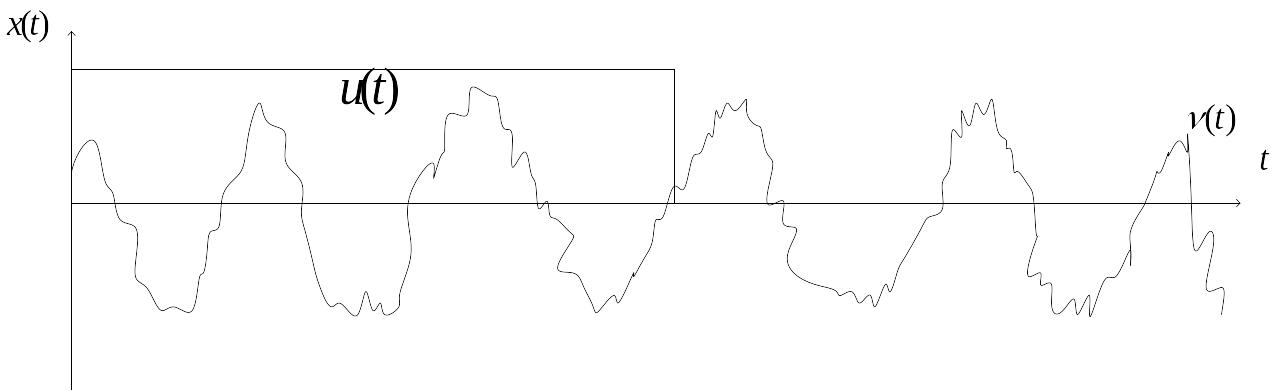
Рис. 12.3

Следовательно, преобразование Фурье функции есть свёртка преобразования функций и :

В свою очередь, преобразование Фурье прямоугольной функции будет иметь вид:

Рис. 12.4

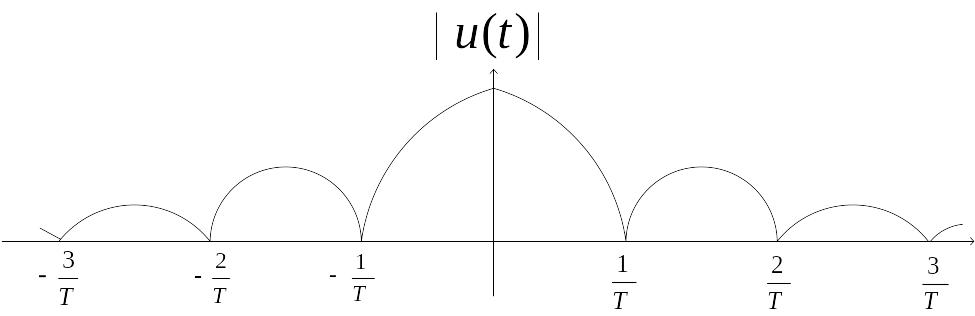
Рис. 12.5

Отметим, что описанная функция представляет собой основное спектральное окно, используемое при анализе. Большие боковые максимумы функции | | обусловливают большое просачивание энергии с частот, далёких от главного максимума спектрального окна и могут привести к сильным искажениям спектральной оценки, особенно заметным для процессов с узкополосным спектром. Проблема просачивания не возникает при анализе периодических процессов (с периодом Т_р).

Для подавления просачивания обычно используют временные окна, сглаживающие исходную реализацию таким образом, чтобы подавить резкие вариации на её начальном и конечном участках.

Существует множество таких окон, но одно из наиболее ранних и широко используемых – косинусоидальное сглаживающее окно, называемое окном Ханна.

Рис. 12.6

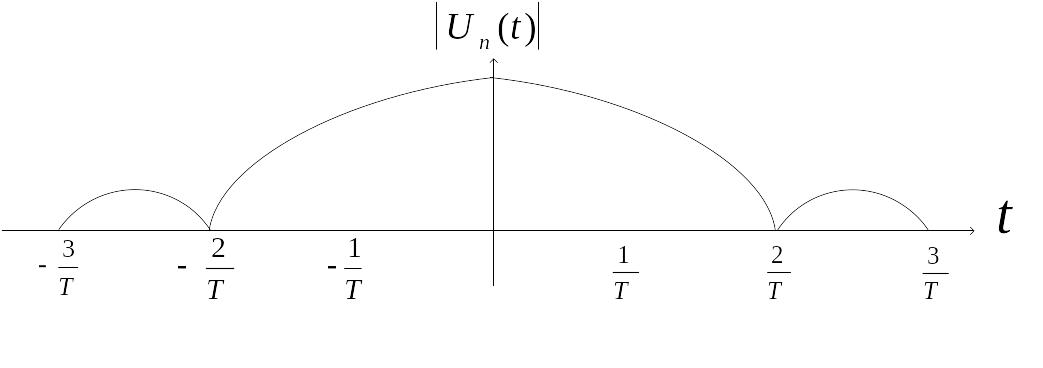
Рис. 12.7

В этом случае .

Её преобразование Фурье есть

Для дискретных значений частоты при получим:

где

Предположим, что в пределах каждой полосы частот шириной функция ведёт себя как ограниченный по частоте белый шум. Тогда математическое ожидание произведения и , вычисленное для любых частот и из набора

С учётом этого свойства

при любых .

Эта величина характеризует потери, вызванные использованием спектрального окна Ханна для оценки спектральной плотности при помощи конечного преобразования Фурье. Поэтому при оценивании спектров необходимо умножение на масштабный множитель . В частности при вычислении спектральной плотности по формуле (12.3) с использованием окна Ханна следует использовать соотношение

Для вычисления оценки СПМ необходимо использовать следующие этапы:

1. Имеющаяся реализация разбивается на отрезков, каждый из которых содержит N отсчётов.

2. При необходимости подавить просачивание энергии через боковые максимумы каждый отрезок сглаживается фильтром, или весовым окном Ханна, или другим подходящим образом выбранным фильтром (к примеру, Баттерворта, Сорта, Хэмминга, Дольфа-Чебышева и т.д).

3. Для каждого отрезка реализации выбирается N значений БПФ .

4. Значения умножаются на масштабный коэффициент для компенсации изменений, внесённых сглаживанием (при использовании окна Ханна этот коэффициент равен ).

5. По формулам (12.4) и (12.5) вычисляется соответственно оценка двусторонней и односторонней спектральной плотности для отрезков.

Косвенный способ оценивания ковариационной функции основан на использовании соотношения Винера – Хинчина. Оценка ковариационной функции находится как обратное преобразование Фурье спектральной плотности.

В случае дискретной последовательности циклическая ковариационная функция принимает вид:

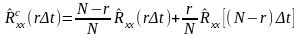
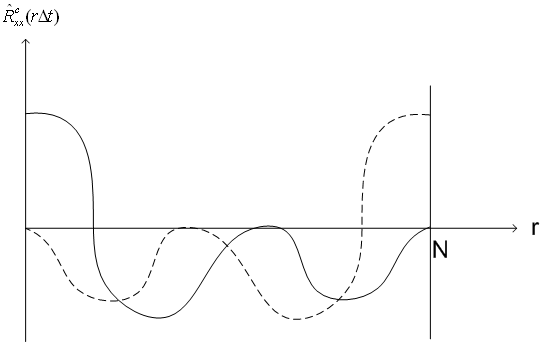
Рис. 12.8

Как видно из рисунка, имеет место эффект наложения. Этого осложнения можно избежать, дополняя исходный временной ряд нулями. В результате этого происходит разделение обеих частей циклической оценки ковариационной функции.

В частности, при добавлении N нулей к исходному временному ряду той же длины будет иметь место полное разделение, т.е.

Заметим, что первая половина этой оценки при представляет собой значения ковариационной функции при положительных значениях сдвига ( ), а вторая ( ) при отрицательных значениях сдвига. Но поскольку ковариационная функция есть функция чётная, то вторую половину можно отбросить и окончательно несмещённая оценка ковариационной функции находится в виде

Полученная оценка статистически эквивалентна прямой оценке (непосредственно по реализации случайного процесса). Однако, в зависимости от величины её такой косвенный метод с использованием БПФ может потребовать заметно меньшего объёма вычислений. Действительно, косвенный метод требует нахождения вначале оценки спектральной плотности мощности, для чего осуществляется БПФ по независимым реализациям, каждая из которых содержит N отсчётов и дополнена N нулями, так что БПФ производится для реализации длиной 2N. Затем 2N значений сглаженной спектральной оценки подвергаются обратному преобразованию Фурье, что в общей сложности даёт ( +1) быстрых преобразований Фурье, каждое из которых требует 4Np операций над действительными числами, где . Для реализации прямого метода потребуется m N операций. Следовательно, при одном и том же максимальном сдвиге m=N коэффициент ускорения вычислений равен:

При N=1024 .

Оценки взаимных корреляционных функций так же, как и оценки автоковариационных функций могут быть получены двумя основными способами: непосредственным вычислением и с использованием БПФ.

• Непосредственное вычисление.

В этом случае несмещённые оценки взаимных ковариационных функций при сдвигах ( ) находятся в виде

Выборочную взаимную ковариационную функцию можно нормировать так? что значения её будут находиться между -1 и +1, для чего необходимо разделить её на величину . Таким образом, получается нормированная взаимная корреляционная функция:

?

rоторая теоретически должна удовлетворять равенству . Аналогично определяется функция .

• Для получения взаимной ковариационной функции при помощи БПФ можно рекомендовать следующую последовательность вычислений. Пусть объём каждой выборки из реализаций x(t) и y(t) составляет чисел. Взаимную ковариационную функцию в этом варианте находят по спектральной мощности процесса, для чего дважды применяют БПФ – к функции x(t) и к функции y(t). Оба преобразования можно получить одновременно, приравняв одну реализацию действительной, а другую мнимой части некоторой комплексной реализации:

? .

Тогда преобразование Фурье функции будет иметь вид:

и может быть вычислено по алгоритму БПФ. Следует отметить, что

Поскольку при любых .

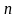Следовательно, комплексно сопряжённая функция равна:

Тогда

Таким образом, преобразования Фурье 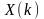и двух действительных реализаций и будут иметь вид:

Этим же приёмом можно воспользоваться для расчёта преобразования на интервале вдвое большей длины. Для этого вещественная реализация ( ) разделяется на две части: одна состоит из значений при чётном , другая – при нечётном. Иными словами:

Рекомендуемая в итоге последовательность операций для получения оценки взаимной ковариационной функции основана на предположении, что длина исходных реализаций , есть , .

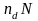1. Выбирается максимальный сдвиг и исходные реализации разбиваются на отрезков, каждый из которых состоит из отсчётов.

2. Каждый отрезок , , дополняется N нулями, в результате чего новый отрезок содержит 2N отсчётов.

3. По отрезкам, содержащим по 2N точек в соответствии с

Методом БПФ вычисляются коэффициенты .

4. На основе соотношений

Вычисляются и .

5. По методу оценивания взаимной спектральной плотности мощности вычисляется оценка двухсторонней спектральной плотности.

6. На основе соотношения

вычисляется обратное БПФ последовательности , дающее оценку , .

7. Несмещённая оценка взаимной ковариационной функции при положительном сдвиге находится умножением на масштабные коэффициенты .

8. Несмещённая оценка взаимной ковариационной функции при отрицательном сдвиге находится умножением на масштабные коэффициенты ( ).

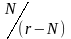По аналогии с оцениванием автоспектров можно рассматривать следующие этапы оценивания функций взаимной спектральной плотности:

1. Имеющиеся реализации разделяются на отрезков , , каждый из которых содержит N отсчётов.

2. При необходимости подавить просачивание энергии через боковые максимумы каждый отрезок , ( ) сглаживается фильтром Ханна или любым другим подходящим образом выбранным фильтром.

3. Сглаженные значения запоминаются как действительная часть, а сглаженные значения - как мнимая часть последовательности ( ).

4. По формуле

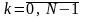
для каждого отрезка вычисляются N значений БПФ .

5. По формулам

для каждого отрезка вычисляются коэффициенты и , .

6. Значения и умножаются на масштабный коэффициент для компенсации внесённых сглаживанием изменений (при использовании окна Ханна этот коэффициент равен ).

7. Для каждой пары отрезков по значениям , вычисляется оценка двухсторонней взаимной спектральной плотности

или односторонней взаимной спектральной плотности

8. Осреднение оценок по парам отрезков даёт окончательную сглаженную оценку ( ) или ( ).