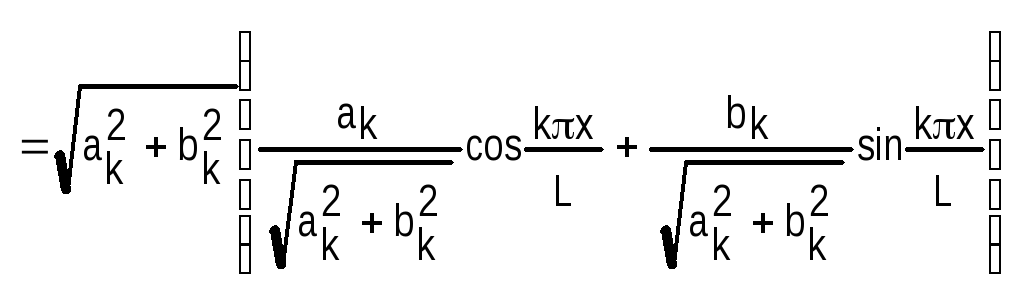ответы на тесты, билеты / ответы на экзаменационные вопросы, 3 семестр, ратафьева / mat_5_#3

sin(mx)

Аналогично, f(x) sin(mx), получим:

. При этом при m=k:

24, Разложение в ряд Фурье функций, заденных на промежудке [0;l]

Допустим, что на промежутке [0;L] функция удовлетворяет условиям теоремы Дирихле, и нам нужно разложить её в ряд Фурье. Для этого мы должны доопределить её на отрезке [-L;0]. Если не поставлены никакие ограничения, то доопределение может быть произведено.

1. Доопределение чётным образом.

Доопределение нечётным образом.

Пример см.на шпоре

Обозначим:

Тогда исходное выражение примет вид:

Это представляет собой гармоническое колебание с амплитудой и частотой

Под знаком суммы в тригонометрическом ряде Фурье содержатся наложенные друг на друга гармонические колебания. Амплитуды и частоты меняются. Если к стремится к бесконечности, то и ω_к стремится к бесконечности.

Пусть L стремится к бесконечности. Рассмотрим, как можно осмыслить тригонометрический ряд Фурье. Дальнейшее рассуждение будет носить нестрогий характер, однако оно хорошо проясняет физическую суть вопроса.

Наложим дополнительные ограничения на функцию f(x).

1. Она ограничена на всей числовой оси.

2. Несобственный интегралсходится, т.е. функция абсолютно интегрируема на всей числовой оси.

В дальнейшем проведём рассуждения, предполагая, что функция стремится к плюс бесконечности, перейдя таким образом от [-L;+L] к (-∞;+∞). Принимая во внимание выражение для коэффициентов ряда Фурье, запишем:

Обозначим:

Обозначаем α_к за α.

Теперь продолжим вычисления:

!!!!!!!!!!!!!!

Получили интегральную сумму по переменной α. В пределе справа получаем двойной несобственный интеграл:

Это и есть интеграл Фурье. Интеграл Фурье есть обобщение ряда Фурье. Заметим, что переменная α стоит под знаком косинуса. По отношению к α подинтегральная функция чётная. Поэтому:

1. 25, Комплексная форма ряда Фурье.

Ранее предположили, что на [-L;L] функция f(x) определена и имеет разложение:

Формула Эйлера:

Подставим систему (3) в ряд Фурье.

Обозначим:

Тогда:

Если функция удовлетворяет условиям теоремы Дирихле, то в точках непрервыности она представима таким рядом:

ЭТО КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ

Комплексная форма ряда Фурье

Заметим, что от ряда Фурье в комплексной форме без труда можно перейти к ряду Фурье в тригонометрической форме. Для этого надо учесть следующий факт:

Домножим числитель и знаменатель на сопряжённое знаменателя:

22, Разложение в тригонометрический ряд на промежудке [-l;l]

Пусть функция f(x) определена на [-l;+l].

Если функция удовлетворяет условиям теоремы Дирихле, то для неё можно построить ряд Фурье.

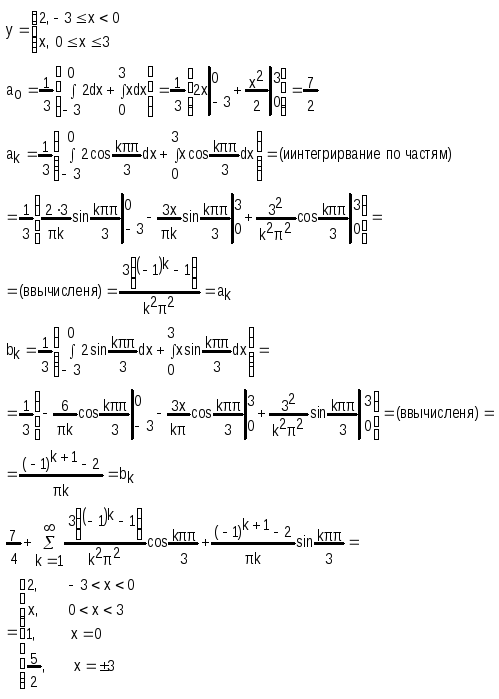
Пример.

23. Ряд Фурье для четных и нечетных функций.

Пусть функция f(x) определена на [-a;a]. Пусть эта функция удовлетворяет условиям теоремы Дирихле. Тогда для неё можно построить ряд Фурье.

2. Интеграл Фурье.

Если функция на промежутке [-L;L] удовлетворяет условиям теоремы Дирихле, то она представима в виде ряда:

Рассмотрим отдельно соотношение: