38. Метод проекции градиента задачи условной оптимизации.
(1)
На
каждой итерации этого метода предусмотрена
процедура возврата очередного приближения
градиентного спуска
в мн-во Х, т.е. если
то
заменяют наближайшую точку мн-ва Х.
Опр.
Пусть заданы замкнутое мн-во
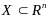и точка
. Точку
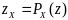будем называть проекцией точки
на мн-во Х, если выполн условие
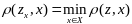, где
- норма в пространстве
Если
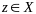, то
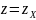. Т.о. в методе проекций градиента
последовательные приближения
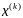целевой функции
на мн-ве Х вычисляется по формулам:
,
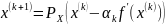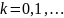(2)
В зависимости от способа вычисления из (2) различают несколько видов метода проекции градиента:
находят из условия наискорейшего спуска безусл оптимизации, т.е.
Если производная целевой ф-ции удовлетворяет усл Липшица на мн-ве Х, т.е.
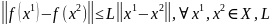-константа
Липшица, то
выбирают постоянным,
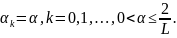
Вычисления
по ф-ле (2) прекращаются при выполнении
одного из условий остановки:
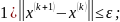
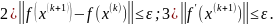
Замечание.
Задача нахождения проекции точки на
мн-во явл. задачей квадратичного
программирования.
Эта
задача технически может вызвать
затруднения.
40. Метод покоординатного спуска для задачи с ограничениями.
Метод повторяет алгоритм метода решения задачи безусловной оптимизации со следующими дополнениями:
Пробная
точка
должна удовл. двум условиям:
1.
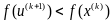; 2.
.
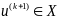Если хотя бы одно из условий не выполняется, то ищем след пробную точку.
Если пробная точка найдена, а точка минимума лежит на границе мн-ва Х, то для обнаружения такой точки минимума потребуется дополнительные условие, к-рое:
1.
В случае дробления шага имеет вид
;
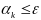2.
в случае выбора
из условия наискорейшего спуска
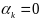
(Метод безусловного покоординатного спуска:
Итерационный
процесс этого метода описывается
формулой
(2)
Шаг выбирается одним из 3-х способов:
1)
постоянный шаг:
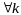(очень грубый, редко применяется);
2)
дробление шага (применяется когда
выполняется условие релаксации
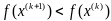, но не выполняется условие остановки.
Тогда шаг дробят одним из 2-х способов:
или
3) шаг выбирается из условия наискорейшего спуска
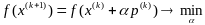(3)
(задача
одномерной минимизации относительно
)
Направление
выбирается вдоль координатных осей.
Изложим одну итерацию метода покоординатного
спуска с дроблением шага: точка
и шаг
известны (наперед заданы). Вычисляем
пробную точку
, где
- вектор, состоящий из нулей, а на
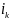месте стоит 1.
(в первую очередь перебираются
положительные направления). Проверим
условия релаксации
. Если оно выпол-ся, то пробную точку
принимаем
за следующую точку приближ, т.е.
.
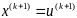Если условия релаксации не выполняются, то меняем направление на противоположное и снова проверяем условия релаксации. Если оно выполняется, то . Если не выполняется, то берем все возможные направления. В противном случае шаг дробим и все повторяем сначала.)
42. Алгоритм решения задачи кп
КП – это раздел, изучающий экстремальные задачи, когда целевая ф-ция явл. квадратичной, ограничения – линейные.
Задачи КП с ограничениями типа равенств.
Задача
имеет вид:
(1),
(2),
где x-
n-вектор,
b-
m-вектор,
А- m×n
матрица, D-
n×n-
симметричная положительная матрица,
rankA=m<n.
По
ф-ции Лагранжа
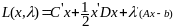составим
двойственную ф-цию:
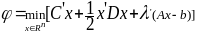(3)
Т.к.
в ф-ле (3) минимизируемая ф-ция строго
выпукла (D>0),
то её точка минимума х(λ)- совпадает со
стационарной точкой ф-ции Лагранжа,
т.е.
.
Используем
ф-лы:
,
,
.
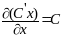Тогда
условие стационарности будет иметь
вид:
;
;
-
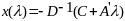точка
минимума задачи (3). Подставим (4) в ф-лы
(3):
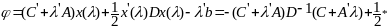
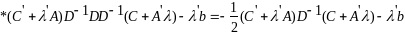(5)
Двойственная
к (1)-(2) задача состоит в максимизации
ф-ции
,
.
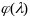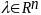Т.к.
для
ф-ции
,
то
ф-ция
явл.
строго вогнутой, тогда её точка максимума
совпадает
со стационарной точкой:
.
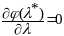Она
получается из тех же преобразований,
что были предложены выше и
.
Задача КП с ограничениями типа неравенств.
Эта
задача имеет вид:
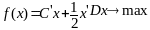(1),
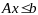(2) ,
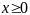(3),
где D-
симметричная отрицательно определённая
м-ца, значит кв-я форма
-
вогнута,
задача (1)-(3)- задача выпуклого
программирования.
Т-ма.
Вектор
явл.
оптимальным решением задачи (1)-(2) т. и
т.т.,к. существуют m-мерные
векторы
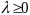и
и
n-мерный
вектор
,
что
выполн. условия: 1)
;
2)
;
3)
;
4)
.
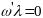Для нахождения нач. базисного плана решения ситемы
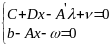применяется
М-метод введения искусственных переменных:
n-вектора
z
и m-вектора
y.
Тогда условия 1) и 2) будут иметь вид:
.
Выбрав
компоненты в-ров z
и y
одинакового знака со знаками свободных
слагаемых – С и b,
находим нач. базисное решение. Если
,
,
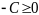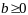то
нач. базисный план
.
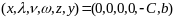Составим
целевую ф-цию:
,
где
М>0.
Решим
задачу:
,
,
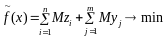где
.
(4) Задача
(4)- задача ЛП, которую можно решить
симплекс-методом. Если удаётся вывести
все искусственные переменные и при этом
выполнить усл. 3) и 4) теоремы, то найденное
базисное решение будет оптимальным.