14. Классификация задач линейного программирования. Основные понятия.

Линейное программирование (ЛП) – раздел математики, в котором изучаются задачи оптимизации с линейной целевой ф-цией и ограничениями заданными сис-мой линейных равенств или неравенств.

Различают две формы задач ЛП:

1. задача ЛП в канонической форме (стандартной форме)

. (1)

2. задача ЛП в нормальной форме

. (2)

- -вектор, - -вектор неизвестных, -матрица, - -вектор столбец.

Все остальные задачи ЛП сводятся к одной из этих форм.

Задачу ЛП можно решить только в том случае, если она сведена к канонической форме. Задачу ЛП решают симплекс-методом. Понятие симплекс-метода строится на основе понятия базисного плана. Симплекс-метод представляет собой симплексные итерации (переходы) от одного базисного плана к другому.

Определение. -вектор называется планом задачи (1), если он удовлетворяет основным ( ) и прямым ( ) ограничениям.

Определение. План называется базисным планом задачи (1), если его компоненты равны нулю, а остальным его компонентам соответствуют линейно независимые столбцы матрицы .

Т.о. вектор разбивается на два подвектора (Н - небазисное, Б - базисное); мн-во индексов, которое состояло разобьется на , , ,

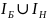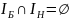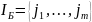Соответственно на базисные и небазисные компоненты разобьются м-ца А и С.

. По определению базисного плана, план – базисный план, если

Определение. Базисный план называется невырожденным, если , .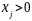

Определение. План называется оптимальным базисным планом задачи (1), если

.

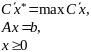16. Формула приращения целевой функции в задаче линейного программирования (лп).

Рассмотрим задачу . (1)

Пусть – базисный план этой задачи с базисной матрицей . Рассмотрим план , который строится по формуле . Найдём значение приращения целевой функции при переходе базисного плана к плану .

Таким образом

. Введем обозначения Тогда

 - наз. -оценкой базисного плана .

Физический смысл: оценка, взятая с противоположным знаком - означает приращение целевой функции при переходе от плана к плану , когда увеличивается небазисная компонента ,

Замечание.

Общее св-во компонент базисного плана.

18. Достаточное условие неразрешимости злп.

Пусть x – базисный план с базисной матрицей А_Б и критерий оптимальности не выполняется, н-р, по j₀ компоненте, т.е. Δ j₀<0, j₀ЄI_н (небазисная компонента). Обозначим компоненты вектора и предположим, что они не положительны. Тогда из док-ва критерия оптимальности следует для любых планов . Рассм. приращения целевой ф-ции . .

Т.о. доказали теорему:

Теорема. (Достаточное условие неразрешимости ЗЛП).

Если на базисном плане x критерий оптимальности не выполняется по j₀ компоненте и , , то целевая функция неограниченно возрастает, зн. ЗЛП не имеет решения.