
- •2. Классификация задач оптимизации. Примеры.
- •Полная классификация задач оптимизации
- •4. Задача безусловной оптимизации (збуо). Необходимые условия оптимальности.
- •6. Задача условной оптимизации с ограничениями типа равенств. Метод исключения.
- •8. Классическое правило множителей Лагранжа в задаче с ограничениями типа равенств.
- •12. Необходимое условие минимума 2-го порядка для гладких задач на условный минимум с ограничениями типа неравенств.
- •14. Классификация задач линейного программирования. Основные понятия.
- •16. Формула приращения целевой функции в задаче линейного программирования (лп).
- •18. Достаточное условие неразрешимости злп.
- •20. Конечность симплекс-метода. Зацикливание. Геометрическая интерпретация симплекс-метода.
- •22. Двойственная задача. Теория двойственности лп.
- •26. Выпуклые множества и их свойства.
- •28. Основная задача выпуклого программирования. Необходимое условие существования седловой точки.
- •30. Задача одномерной оптимизации. Классический метод.
- •32. Задача одномерной оптимизации. Метод «золотого сечения».
- •34. Задача одномерной оптимизации. Метод касательных
- •36. Градиентный метод безусловной оптимизации.
- •38. Метод проекции градиента задачи условной оптимизации.
- •40. Метод покоординатного спуска для задачи с ограничениями.
- •42. Алгоритм решения задачи кп
- •44.Предмет ви. Задача о брахистохроне.
- •46. Метод вариации основной задачи ви. Вариации кривой и функционала.
2. Классификация задач оптимизации. Примеры.
Полная классификация задач оптимизации
Задачи математического программирования (конечномерные задачи).
Линейное программирование (f(x) – линейная, X – система линейных равенств или неравенств).
Задачи нелинейного программирования.
- безусловной оптимизации;
- условной оптимизации с ограничениями типа равенств;
- условной оптимизации смешанного типа;
- условной оптимизации с ограничениями типа неравенств;
- выпуклое программирование (f(x) – выпуклая, X – выпуклое множество);
- квадратичное программирование (f(x) – квадратичная ф-ция, X – система лин. уравнений или неравенств).
c) целочисленное программирование (на вектор x накладывается условие целочисленности).
d) многоэкстремальные задачи (f(x) – m-вектор ф-ция, X – n- вектор).
2. Вариационное исчисление .
 – бесконечномерная
задача.
– бесконечномерная
задача.
Задачи оптимального управления
4. Задача безусловной оптимизации (збуо). Необходимые условия оптимальности.
Постановка
задачи:
 ,
,
 (1)
(1)
Опр.
Говорят,
что
 ,
если
,
если
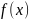 -непрерывна
вместе со всеми производными до к-того
порядка включительно.
-непрерывна
вместе со всеми производными до к-того
порядка включительно.
Теорема (необх. условия лок. опт-ти 1-го порядка).
Пусть
функция f
дифференцируема в
 в точке
в точке
 Если
Если
 точка лок. минимума задачи (1), то выполн.
условие стационарности:
точка лок. минимума задачи (1), то выполн.
условие стационарности:
 (2)
(2)
-стационарная точка, если для нее выполн. (2).
 .
.
Док-во.
 и числа
и числа
 верно разложение ф-ции f
в ряд Тейлора:
верно разложение ф-ции f
в ряд Тейлора:
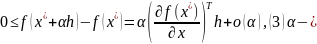 дост.
малое.
дост.
малое.
-
точка лок. минимума, зн.
 .
Поэтому
.
Поэтому
 .
Разделим нер-во (3) на
.
Разделим нер-во (3) на
 ,
,

Используя
 при
при
 получаем
получаем
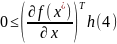 . (4) должно выполн-ся для
. (4) должно выполн-ся для
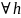 ,
в том числе и при
,
в том числе и при
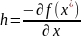 .
Из (4) получаем
.
Из (4) получаем
Поэтому,

|

Теорема (необх. условия опт-ти 2-го порядка).
Пусть
f Если
-
точка лок. минимума задачи (1), то
Если
-
точка лок. минимума задачи (1), то

Док-во.
, имеет место разложение в ряд Тейлора
имеет место разложение в ряд Тейлора
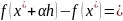
 Делим
нер-во на
Делим
нер-во на
 ,
, ,
,
|


6. Задача условной оптимизации с ограничениями типа равенств. Метод исключения.
ЗУО с ограничениями типа равенств имеет вид:
 (1)
(1)
 -
m
вектор-функция,
-
m
вектор-функция,
 ,
i=1, …,m. Простейшим
методом решения задачи (1) явл. метод
исключения.
,
i=1, …,m. Простейшим
методом решения задачи (1) явл. метод
исключения.
Опр. Точку наз. точкой условного глобального минимума, если

Опр.
Точку
наз. точкой условного локального
минимума, если
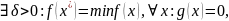

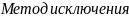 .
Применяется, когда кол-во ограничений
меньше кол-ва переменных, т.е. m
< n,
и вид ограничений
.
Применяется, когда кол-во ограничений
меньше кол-ва переменных, т.е. m
< n,
и вид ограничений
 достаточно простой. В этом случае из m
ограничений можно выразить m
переменных.
достаточно простой. В этом случае из m
ограничений можно выразить m
переменных.
Допустим,
что это переменные ,
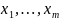 ,
т.е.
,
т.е.

 …,
…,
 (2)
(2)
Подставим в эти формулы целевую ф-цию (1). Получим:


Решая задачу безусловной оптимизации (3) по ур-ниям связкам восстанавливаем переменные .
