1.5 Выводы
Вывод: все построенные модели отвечают условиям адекватности. Наиболее высокие статистические характеристики имеет модель Y=f(X3) вида:
Y=19,46722*1,135417^x, в которой
коэффициент детерминированности R^2=0,964;
критерий Фишера F=242,94 (Fp=242,94>Fтабл=5,12)
критерий Стьюдента =17,79 (tpасч=17,79>tтабл=2,26) коэффициенты уравнения значимы.
Решение задания с помощью встроенных функций библиотеки Stats (Statistics) CKM Maple.
>
Задаем исходные данные:
>
>
>
>
Определяем коэффициенты корреляции между различными наборами данных:
>
>
>
>
>
>
Полученные значения полностью совпадают с матрицей коэффициентов парной корреляции на рис. 2. Вычисляем коэффициент вариации:
>
Вычисляем линейную ковариацию:
>
Вычисляем среднее геометрическое:
>
Вычисляем среднее арифметическое:
>
Вычисляем медиану:
>
Вычисляем квадратичное среднее арифметическое:
>
Дисперсия:
>
Рассчитаем коэффициенты уравнения линейной регрессии и приведем полученное уравнение к численному виду:
>
>
>
Преобразовываем массив Y в данные типа array (массив):
>
Для расчета функциональной зависимости между экспериментальными данными X1 и Y и возможности ее графического отображения определим функцию пользователя spisok=f(x) c использованием функционального оператора à:
>
Для того, чтобы графически отобразить экспериментальные данные и построить линию тренда, значения X1 и Y сначала следует сгруппировать попарно функцией zip:
>
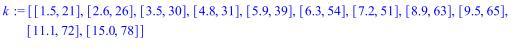
Выделяем правую часть полученной функциональной зависимости f1:
>
Рассчитываем линию тренда Y1:
>
Преобразовываем полученный массив Y1 в данные типа array (массив):
>
Преобразовываем полученный массив Y1 в данные типа list (список):
>
Здесь стандартная функция rhs библиотеки stats выделяет правую часть полученной функциональной зависимости для расчета линии тренда Y1, функция nops в цикле for подсчитывает количество значений X, функция subs осуществляет подстановку значений аргумента из массива X1[i] в уравнение регрессии, а функция convert преобразовывает полученный массив Y1 в данные типа list (список) для возможности использования их в функции построения графика plot. Сопоставляем Х1 и Y1:
>
Заданные в функции plot параметры позволяют не только построить реальную и расчетную зависимости, применив различные графические стили и комментарии, но и вывести на графике уравнение регрессии:
>
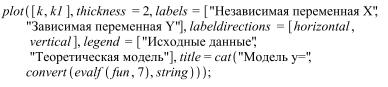
После расчета уравнения регрессии необходимо определить адекватность модели, для чего рассчитывается статистика по регрессии: коэффициент корреляции, коэффициент детерминированности, ошибки по X1 и по Y, остаточная сумма квадратов, регрессионная сумма квадратов, критерий Фишера и некоторые другие.
Подсчитываем количество значений Y:
>
Рассчитываем статистику по линейной регрессии:
>
>
>
>
>
>
>
>
>
>
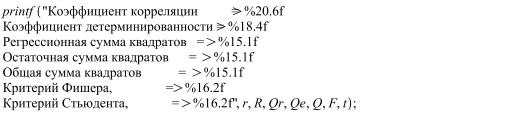
Коэффициент корреляции => 0.961743
Коэффициент детерминированности => 0.9250
Регрессионная сумма квадратов => 3652.7
Остаточная сумма квадратов => 295.8
Общая сумма квадратов => 3941.6
Критерий Фишера, => 111.10
Критерий Стьюдента, => 10.53
Задание 2. Используя компьютерные технологии, решить задачи линейного программирования.
а) Задача оптимального планирования производства
Условие задания 2а): Для производства двух видов изделий А и В используется три типа технологического оборудования. На производство единицы изделия А оборудование первого типа используется а1 часов, оборудование второго типа – а2 часов, оборудование третьего типа – а3 часов. На производство единицы изделия В оборудование первого типа используется в1 часов, оборудование второго типа – в2 часов, оборудование третьего типа – в3 часов.
На изготовление всех изделий администрация предприятия может предоставить оборудование первого типа не более чем на t1 часов, оборудование второго типа не более чем на t2 часов, оборудование третьего типа не более чем на t3 часов. Прибыль от реализации единицы готового изделия А составляет α руб., а изделия В – β руб.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
В качестве инструментария решения использовать:
- надстройку «Поиск решения» ТП MS Excel;
- библиотеки Simplex и Optimization СКМ Maple.
Вариант |
а1 |
а2 |
а3 |
в1 |
в2 |
в3 |
t1 |
t2 |
t3 |
α |
β |
5 |
8 |
6 |
3 |
2 |
3 |
2 |
840 |
870 |
560 |
6 |
2 |
б) Задача оптимизации плана перевозок (транспортная задача)
Условие задания 2б): Имеются n пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции с i-го пункта производства в j-й центр распределения cij приведена в таблице, где под строкой понимается пункт производства, а под столбцом – пункт распределения. Кроме того, в этой таблице в i-той строке указан объем производства в i-м пункте производства, а в j-м столбце указан спрос в j-м центре распределения. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы. Номер таблицы с исходными данными соответствует номеру варианта.
В качестве инструментария решения использовать:
надстройку «Поиск решения» ТП MS Excel,
библиотеку Simplex СКМ Maple,
библиотеку Optimization СКМ Maple.
Вариант 5
|
Стоимость перевозки единицы продукции |
Объёмы производства |
||||
|
3 |
9 |
4 |
5 |
40 |
|
|
1 |
8 |
5 |
3 |
10 |
|
|
7 |
2 |
1 |
4 |
30 |
|
|
2 |
4 |
10 |
6 |
20 |
|
Объёмы потребления |
50 |
10 |
30 |
10 |
|
|
|
|
|
|
|
|
|
Решение задания 2.
а) Задача оптимального планирования производства
Решение задания 2 предполагает:
1. Математическую постановку задачи.
2. Размещение на рабочем листе ТП MS Excel исходных данных, расчёт значений ограничений, расчёт значений целевой функции.
3. Формулировка математической модели задачи в терминах ячеек рабочего листа ТП MS Excel.
4. Поиск оптимального решения поставленной задачи средствами надстройки «Поиск решения».
5. Анализ результатов.