§ 3.1. Определение реакции опор двухопорных балках

Для определения опорных реакций необходимо составить уравнения равновесия сил и моментов и решить их относительно неизвестных реакций.

Для равновесия плоской системы сил, необходимо, чтобы алгебраическая сумма проекций всех сил этой системы на каждую из двух координатных осей равнялась нулю и алгебраическая сумма моментов сил относительно опор А и Д (рис.3.3 ) равнялись нулю.

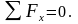
Пример 3.1. Определить опорные реакции балки при следующих данных: АВ = а = 0,3м, ВС = 0,5м, СД = 0,2 м, F₁ = 10кН, F₂ = 20 kH, α = 60⁰ (Рис.3.3).

Cоставляем и решаем уравнения равновесия:

∑Х = 0; ∑У = 0; ∑М_А = 0; ∑М_Д = 0.

а) Определяем проекции сил на оси действующие на балку:

Уравнение равновесия системы сил: ∑Х = 0; ∑У = 0;

∑Х = F_2X - R_AX = 0, R_AX = - F₂·Cos α = - 20·Cos 60⁰ = - 20·0,5 = - 10 кН.

Сила F₂, приложенная к балке АД, создаёт реакцию только в опоре А (неподвижная опора) горизонтальную R_AX = -10 кН.

Силы F₁ и F₂, приложенные к балке АД, создают в опорах А и Д вертикальные реакции.

∑У = 0. ∑У = -F₁ – F₂ Sin60⁰ = -F₁– F₂ ∙ sin 60⁰ + R_A + R_D =

= -10 – 20∙0,866 + R_A + R_D = - 37,32 + R_A + R_D = 0.

б) Определяем реакции опор R_А и R_Д

Правило знаков. Момент принято считать положительным, если сила стремиться вращать тело против часовой стрелки, а отрицательный – по часовой стрелке.

Уравнение равновесия системы моментов сил:

∑М_А = 0; ∑М_Д = 0.

Предполагаем, что реакции опор положительны, т.е. направлены в положительном направлении оси У.

Р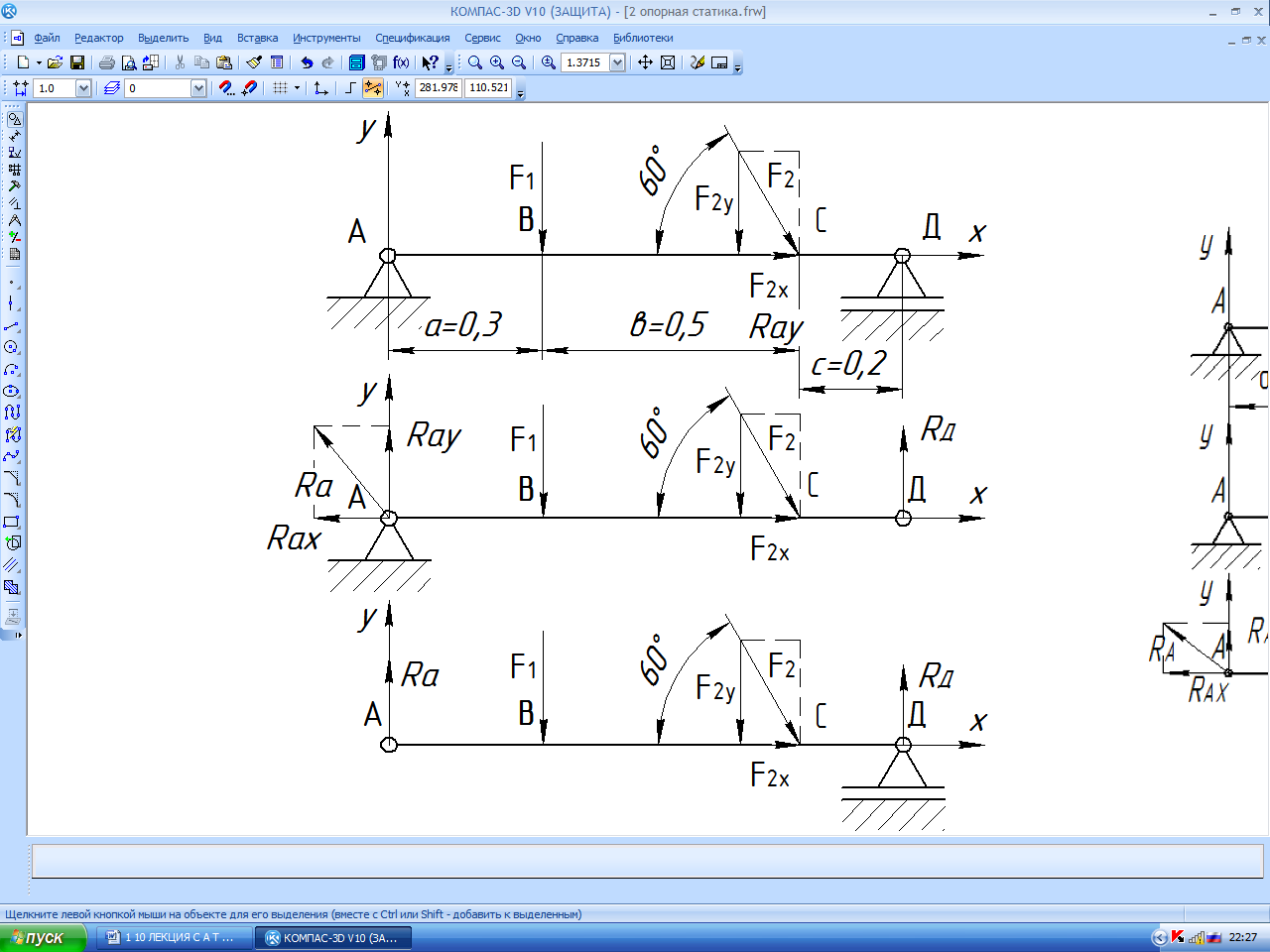 ис.3.3

Мысленно отбрасываем опору Д внешнюю нагрузку действующую на опору Д заменяем реакцией опорой R_Д.

∑М_А = 0;

∑М_А = - F₁×а – F₂×Sin α×(а+в)+R_Д×(а+в+с) =

=- 100,3 – 20×0,866 × ×0,8+ 1хR_Д = - 3 – 13,856 + R_Д = 0

R_Д = 16,856 кН.

Мысленно восстановив опору Д, отбрасываем опору А внешнюю нагрузку действующую на опору А заменяем реакцией опорой R_А.

∑М_Д = 0.

∑М_Д = - R_АY ∙ (а+в+с) + F₁ ∙ (в+с) +F₂ ∙ Sin ∙ с =

=- R_АY ∙ 1 + 10∙0,7 + 20∙0,866∙ 0,2 = - R_АY+7+3,464кН.

R_aY = 10,464 кН.

Проверка: ∑У = 0;

∑У = R_А + R_Д - F₁ – F₂ Sin α =10,464 + 16,856 – 10 -17,32 = 0.

Пример 3.2. Определить опорные реакции балки (рис.3.4) при следующих данных:

F = 10 kH; g = 1 kH/м; М = 20 кН·м; АВ = 1 м; ВД = 2 м; ДЗ = 1 м.

Cоставляем и решаем уравнения равновесия:

∑Х = 0; ∑У = 0; ∑М_В = 0; ∑М_Д = 0.

Проекции на ось ∑Х = 0;

Проекция от сосредоточенной силы F на ось Х равна нулю.

Проекции равномерно распределенной нагрузки g на ось Х равны нулю. Сумма проекций сил пары на любую ось равны нулю.

Проекции на ось ∑У = 0.

B точке А приложена сосредоточенная сила F, проекция на ось У равна модулю силы F;

Рис.3.4

• участок ВД. Заменяем равномерно распределённую нагрузку равнодействующей (сосредоточенной силой) Fg₁ = g ВД = 1 2 = 2 кН, которая проходит через середину участка ВД и приложена в точке С;

• на участке ДЗ. Заменяем равномерно распределённую нагрузку равнодействующей (сосредоточенной силой) Fg₂ = g·ДЗ = 1 1 =1 кН, которая проходит через середину участка ДЗ и приложена в точке Е; в точке З приложена пара сил. Сумма проекций сил пары на любую ось равны нулю.

Предполагаем, что реакции опор положительны, т.е. направлены в положительном направлении оси У.

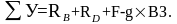
Определяем реакции опор.

∑М_В = 0;

∑М_В = - F·АВ – Fg₁ ВС + R_Д  ВД – Fg₂  ВЕ – М =

=-10· 1 – 1· 2 + R_Д · 2 – 2,5 1 – 20 =

=-10 – 2 + 2 R_Д – 2,5 – 20 = 2 R_Д – 34,5. 2 R_Д = 34,5 кН.

R_Д = 17,25кН.

∑М_Д = 0.

∑М_Д = - F ·АД – R_В · ВД + Fg₁ ·СД – Fg₂ ·ДЕ - М = -10∙3 – 2 R_В + 2∙1 – 1∙0,5 –20. 2 R_В = -48,5 кН.

R_В = -24,25 кН.

Знак минус означает, что принятое направление реакции опоры R_В предварительно принятое нами, по полученным расчётам имеет противоположное направление.

Проверка. ∑Х = 0; Проекции на ось Х равны нулю.

∑У = 0; ∑У = F – R_В - Fg₁ + R_Д - Fg₂ = 10 - 24,25 – 2 + 17,25 – 1 = 0.