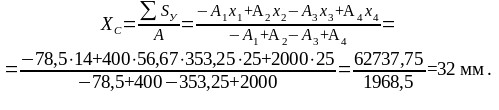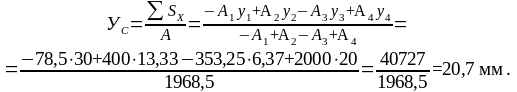§ 14.5. Определение центра тяжести поперечного сечения

Пример 14.4. Для поперечного сечения (Рис.) определить:

Статический момент площади поперечного сечения;

Координаты центра тяжести поперечного сечения.

Направим вспомогательные оси х_в и у_в, относительно которых будем вести отсчёт, по наружным граням поперечного сечения.

Разбиваем сечение на простые фигуры.

Определяем площадь сечения поперечного сечения (рис.4)

Площадь сечения вертикального прямоугольника. А₁ = 2 х 6 = 12 см²:

Площадь сечения горизонтального прямоугольника. А₂ = 5 х 1,5 = 7,5 см²;

Площадь поперечного сечения. А = А₁ + А₂ = 12 + 7,5 = 19,5 см².

1. Определяем координаты центра тяжести поперечного сечения.

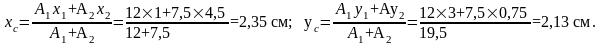
Р ис.14.8

х₁ и у₁ – главные центральные оси сечения вертикального прямоугольника;

х₂ и у₂ – главные центральные оси сечения горизонтального прямоугольника;

х_С и у_С – главные центральные оси поперечного сечения.

Главные центральные оси проходят через центр тяжести сечения, центробежный момент инерции относительно начала координат этих осей равен нулю.

Пример 14.5. На рис.64 изображено плоское сечение пластины состоящей из нескольких геометрических фигур. Требуется определить центр тяжести пластины (рис.64).

В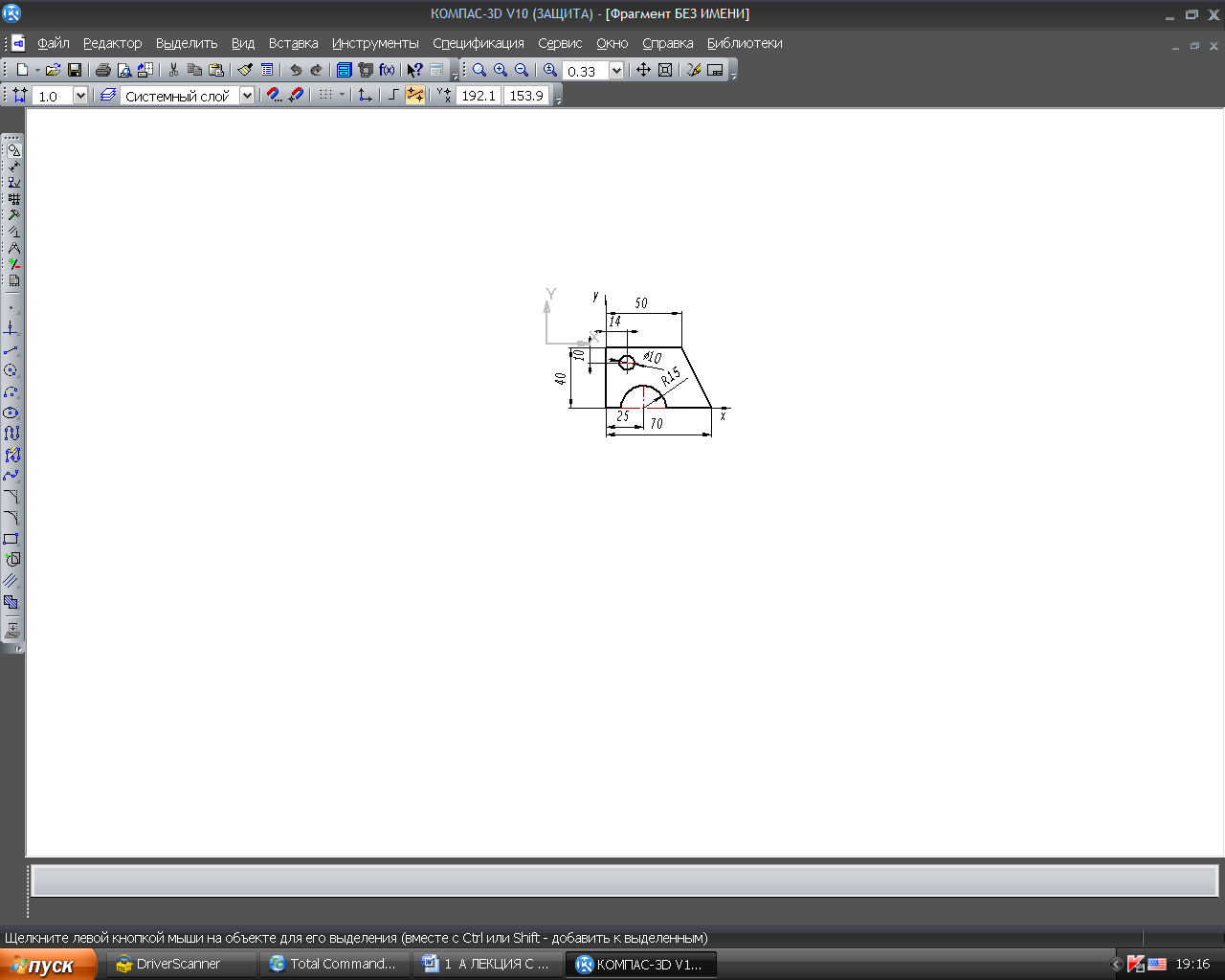 ведём систему координат ХУ (Рис.14.9).

1. Определим площадь и центры тяжести геометрических фигур, составляющих форму пластинки.

Сложные сечения можно разбить на простейшие части (прямоугольник, треугольник, круг и др.), площади и координаты центров тяжести, которых известны, статический момент сложного сечения равен сумме статических моментов составляющих частей:

Рис.14.9

S_X = A₁y₁ + A₂y₂ +…+ A_ny_n.

S_Y = A₁x₁ + A₂x₂ +…+ A_nx_n.

2. Определение статические моменты относительно осей Х и У:

S_Y = -A₁ ∙ x1 + A₂ ∙ x₂ - А₃ ∙ х₃+ А₄ ∙ х₄ =

-78,514 + 400∙(50+6,67) - 353,25 ∙25 + 2000∙25 =

= -1099 + 22668 – 8831,25 + 50000 = 62737, 75 мм³.

Статический момент имеет единицы длины в третьей степени (м³, обычно см³). В зависимости от знака координат он может принимать как положительные, так и отрицательные значения.

S_Х = A₁y₁ + A₂y₂ +А₃у₃ + А₄у₄ =

=-78,530 + 40013,33 - 353,256,37 + 200020 =

=-2355 + 5332 – 2250 + 40000 = 40727 мм³.

Площадь круга:

А ₁ = R² = 3,14 5² = 78,5 мм² (рис.65)

Х₁=5 мм; У₁=5 мм.

Рис.14.10

П лощадь треугольника:

А₂= (bh) : 2 = (2040):2 = 400 мм².

Центр тяжести площади прямоугольного треугольника лежит на одной из его медиан на расстоянии 2/3 этой медианы от вершины треугольника. Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равной одной трети соответствующей

высоты.

Рис.14.11

Х₂ = b/3 = 20/3 = 6,67 мм. У₂ = h/3 = 20/3 = 13,33 мм.

Площадь полуокружности.

А₃= R²/2 = 3,1415²/2 = 353,25 мм².

Центр тяжести полуокружности: Х₃=15 мм.

Р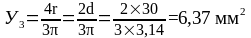 ис.14.12

Площадь прямоугольника. А₄ = 4050 = 2000 мм².

Центр тяжести прямоугольника: Х₄ = 50:2 = 25 мм. У₄ = 40:2 = 20 мм.

Р ис.14.13

Координаты центра тяжести плоской фигуры определяются по формулам:

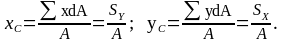
Где Sx и Sy – статические моменты относительно осей Х и У; А –площадь поперечного сечения; dA – площадь составляющих сечений; Х и У– расстояния от центра тяжести составляющих сечений, соответственно до оси Х и У.

Зная статические моменты поперечного сечения, можно вычислить координаты центра тяжести сечения относительно выбранных осей: