§ 14.2. Сложение двух неравных параллельных сил, направленных в разные стороны

Пример14.2. К телу в точках А и В (рис.14.3) приложены две параллельные и направленные в противоположные стороны силы F₁=100 Н и F₂=50 Н.

Определить модуль и линию действия равнодействующей, если расстояние между линиями действия данных сил l=1,2 м.

Модуль равнодействующей R=100-50=50H.

Равнодействующая лежит за большей силой и направлена в сторону большей силы. Обозначим расстояние линии действия равнодействующей R от линии действия большей силы через Х, будем иметь

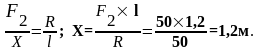
Равнодействующая двух параллельных сил, не равных по модулю и направленных в разные стороны, равна по модулю разности модулей этих сил и направлена в сторону большей силы.

Рис.14.3

Линия действия равнодействующей делит внешним образом расстояние между линиями действия данных сил на части, обратно пропорциональные этим силам.

Система двух параллельных сил, равных по модулю и направленных в разные стороны, называется парой сил.

§ 14.3. Разложение силы на две параллельные составляющие

Любая сила может быть разложена на две параллельные составляющие силы или более. Необходимость разложения сил на параллельные составл яющие возникает в том случае, когда требуется определить усилия в параллельно расположенных элементах конструкции от одной сосредоточенной внешней нагрузки.

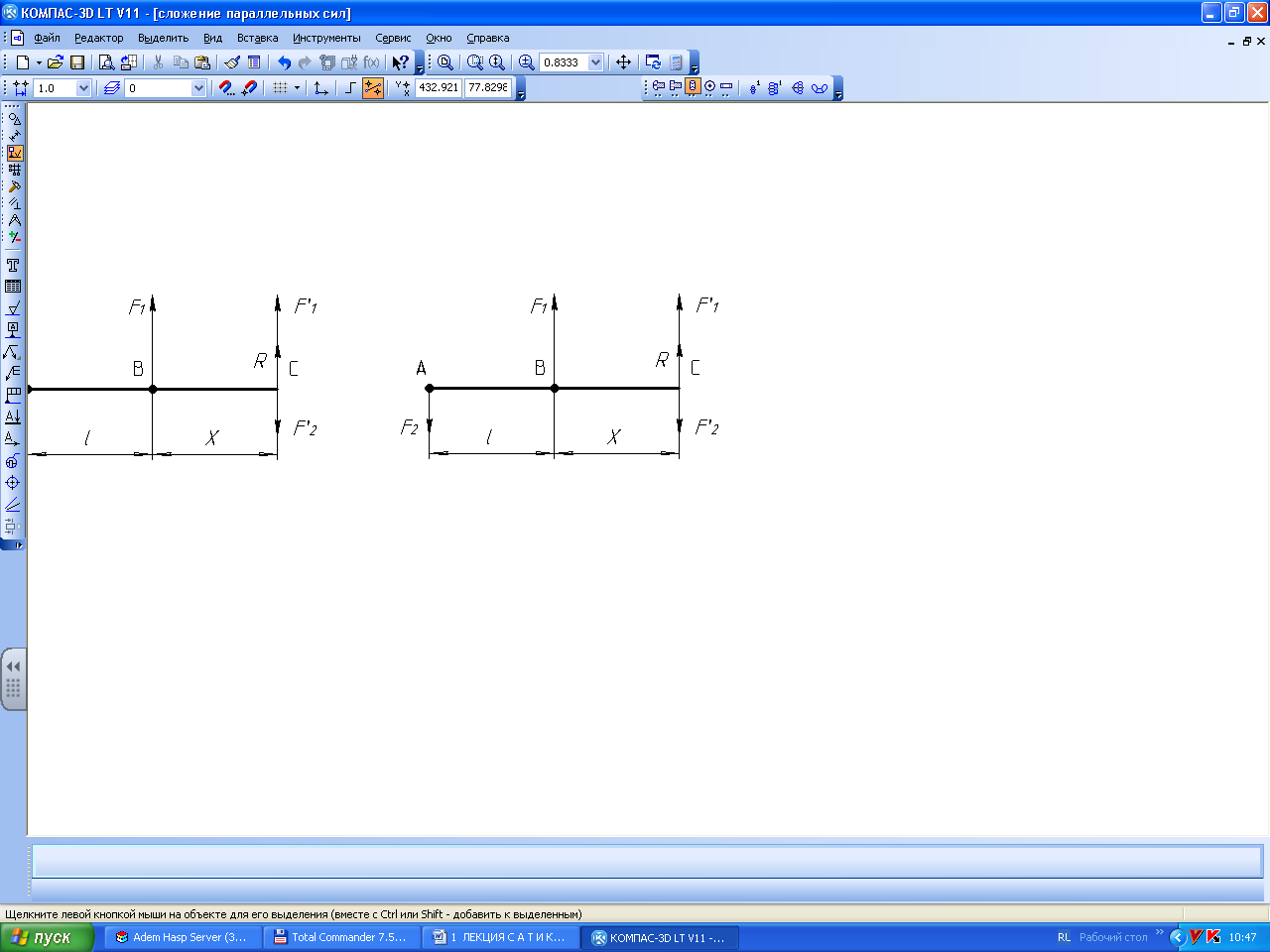
Пример 14.3 К балке подвешенной на двух стержнях требуется подвесить груз R=10кН. Расстояние между стержнями ℓ=5м. В какой точке С нужно подвесить груз, чтобы нагрузка на менее прочный стержень А не превышал 2кН.

Так как R=F₁+F₂=10кН, то F₁=R-F₂=10-2=8кН.

Рис.14.4

Таким образом, модули параллельных составляющих, на которые разлагается сила R, нам известны. В этом случае расстояние АС определяется из пропорции:

§ 14.4. Центр параллельных сил. Центр тяжести

При сложении, каких угодно параллельных сил на векторе равнодействующей всегда получается точка, обладающая важным свойством: она не изменяет своего положения относительно точек приложения составляющих сил, как бы не поворачивались параллельные силы, сохраняя свою параллельность, относительно своих точек приложения.

Действительно, если, например, повернуть силы F₁, F₂ (рис.14.5) относительно их точек приложения в одном направлении и на один угол  и выполнить последовательное сложение этих сил, то на такой же угол окажется повёрнутой и их общая равнодействующая R, но точка её приложения останется неизменной.

Точка, через которую проходит вектор равнодействующей системы параллельных сил при любом повороте этой системы вокруг их точек приложения при сохранении модулей и параллельности векторов, называется центром параллельных сил.

Г рафический способ нахождения центра тяжести сложной плоской фигуры состоит в следующем: данную фигуру разбивают на несколько таких частей простейшей геометрической формы, положение центров, тяжести которых известно. Если данная фигура имеет ось симметрии, то решение задачи упрощается, так, как заранее известно, что центр тяжести такой фигуры лежит на этой оси симметрии.

Рис.14.5

По закону всемирного тяготения на все тела находящихся вблизи земной поверхности, действуют силы притяжения их к Земле, т.е. силы их тяжести.

В механике принят способ определения центров тяжести весомых площадей точнее, пластинок. Принимая, что рассматриваемая площадь геометрической фигуры представляет как бы тончайшую равномерной толщины и однородную пластинку. То есть, если мы имеем поперечное сечение однородного тела, то вес его пропорционален его площади (рис.14.6).

Если в точках А, В, С (рис.14.6) на тела действуют параллельные силы F₁, F₂, F₃, то равнодействующая этих сил равна их сумме, параллельна им, направлена в ту же сторону:

По закону всемирного тяготения на все тела находящихся вблизи земной поверхности, действуют силы притяжения их к Земле, т.е. силы их тяжести.

В механике принят способ определения центров тяжести весомых площадей точнее, пластинок. Принимая, что рассматриваемая площадь геометрической фигуры представляет как бы тончайшую равномерной толщины и однородную пластинку. То есть, если мы имеем поперечное сечение однородного тела, то вес его пропорционален его площади (рис.14.6).

Р ис.14.6

Если в точках А, В, С (рис.61) на тела действуют параллельные силы F₁, F₂, F₃, то равнодействующая этих сил равна их сумме, параллельна им, направлена в ту же сторону:

R = F₁ + F₂ + F₃, аналогично

А = А₁ + А₂ + А₃.

Равнодействующая сил F₁, F₂ равна: R₁ = F₁ + F₂, аналогично

А₁₂ = А₁ + А₂. Точка D приложения равнодействующей делит прямую АВ на части, обратно пропорционально этим силам, т.е.:

Затем определяем равнодействующую сил (алгебраическую сумму составляющих поперечных сечений) составляющих геометрическую фигуру складывая, R₁ c F₃:

R = R₁ + F₃, аналогично А = А₁ + А₂ +А₃.

При расчётах на прочность, жёсткость и устойчивость используются геометрические характеристики поперечного сечения стержня: площадь, статические моменты, положение центра тяжести, осевые и полярные моменты инерции, центробежные моменты инерции, осевые и полярные моменты сопротивления и радиусы инерции.

Статический момент площади плоской фигуры относительно произвольной оси, лежащий в той же плоскости, называется распространённая на всю площадь А сумма произведений элементарных площадок dА на их расстояние до этой оси (рис.62):

Координаты центра тяжести плоской фигуры определяются по формулам:

Отсюда S_x = A·y_c; S_y = A·x_c.

Где Sx и Sy – статические моменты относительно осей Х и У;

А – площадь поперечного сечения;

dA – площадь составляющих сечений;

Х и У– расстояния от центра тяжести составляющих сечений, соответственно до оси Х и У.

Статический момент применяется для определения центров тяжести.

Статический момент имеет единицы длины в третьей степени (м³, обычно см³). В зависимости от знака координат он может принимать как положительные, так и отрицательные значения (рис.35). Координаты центра тяжести однородного тела зависят от формы и размеров тела, но не зависят от материала тела.

Сложные сечения можно разбить на простейшие части (прямоугольник, треугольник, круг и др.), площади и координаты центров тяжести, которых известны, статический момент сложного сечения равен сумме статических моментов составляющих частей:

S_X = A₁y₁ + A₂y₂ +…+ A_ny_n.

S_y = A₁x₁ + A₂x₂ +…+ A_nx_n.

Статический момент, относительно любой оси, проходящей через центр тяжести, равен нулю. Оси координат, проходящие через центр тяжести, называются центральными.

Зная статические моменты поперечного сечения, можно вычислить координаты центра тяжести сечения относительно выбранных осей:

Рис.14.7