§ 6.5. Равновесие рычага

В задачах механики часто приходится рассматривать равновесие тела, шарнирно закреплённого на некоторой неподвижной оси. Такое тело называют рычагом.

Р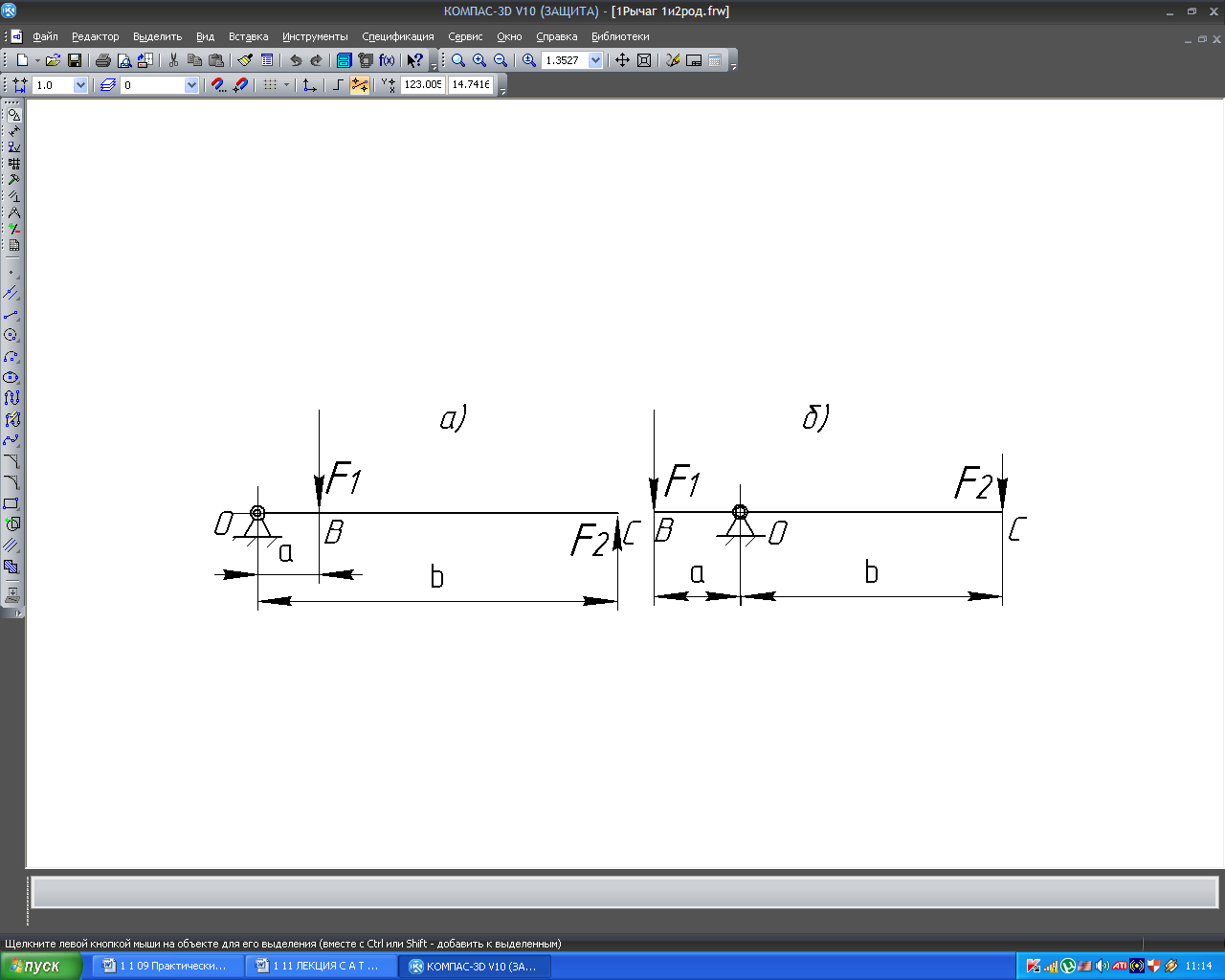 ычаг – это твёрдое тело сравнительно небольшого поперечного сечения при большой длине, имеющее точку опоры и находящееся под действием системы сил.

Рис.6.8

На рисунке 6.8, а) и б) показаны рычаги первого и второго рода, на каждый из которых действует две силы.

Силы, приложенные к рычагу, создают противоположные по направлению моменты относительно его точки опоры. Если эти моменты равны, рычаг остаётся в равновесии.

-F₁·a + F₂·b = 0. F₂·b = F₁·a

Для равновесия рычага необходимо и достаточно, чтобы алгебраическая сумма моментов всех сил относительно точки опоры была равна нулю, т.е.

∑ M_O = -F₁·a + F₂·b = 0.

Золотое правило механики:

Д ля примера (рис.36, а и рис.35, б): F₁ = 250 кН, F₂ = 50 кН, а = 0,1 м.

Определить – b.

Подставим значения 50 х b = 250 х 0,1, откуда

b = (250 х 0,1) : 50 = 0,5 м.

Выиграли в силе F₁ : F₂ = 250 : 50 = 5 раз, проиграли в расстоянии

b : а = 0,5 : 0,1 = 5 раз.

Пример 6.1. На рычаг АЕ (Рис.6.9) действуют силы F₁ = 10кН; F₂=15кН; F₃=20кН; Какой модуль силы F₄ нужно приложить, чтобы рычаг находился бы в равновесии. Остальные данные взять с рисунка.

Для выполнения, чтобы рычаг находился в равновесии, требуется выполнить условие, что алгебраическая сумма моментов относительно центра вращения С равнялась нулю.

∑М_С=0.

∑М_С= F₁∙(a+b)+ F₂∙d₂ + F₃∙d₃ - F₄∙d₄ =

10∙35+15∙20∙sin60⁰+20∙30∙sin60⁰-F₄∙50∙sin45⁰=

=350+300∙0,866+600∙0,866-F₄∙50∙0,707 =

350+259,8+519,6-F₄∙35,35=1129,4-F₄∙35,35=0.

F₄=31,95 kH.

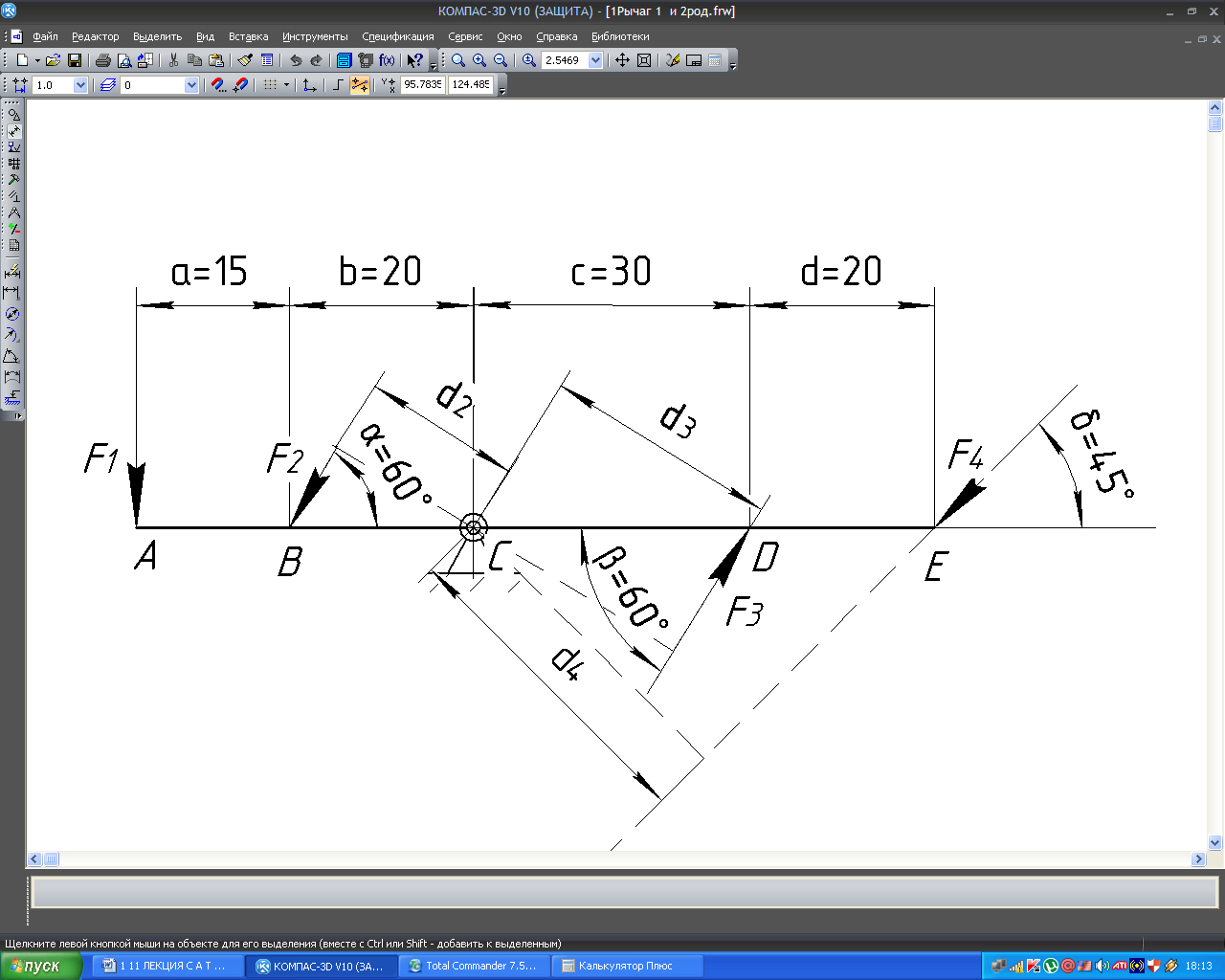Рис.6.9

П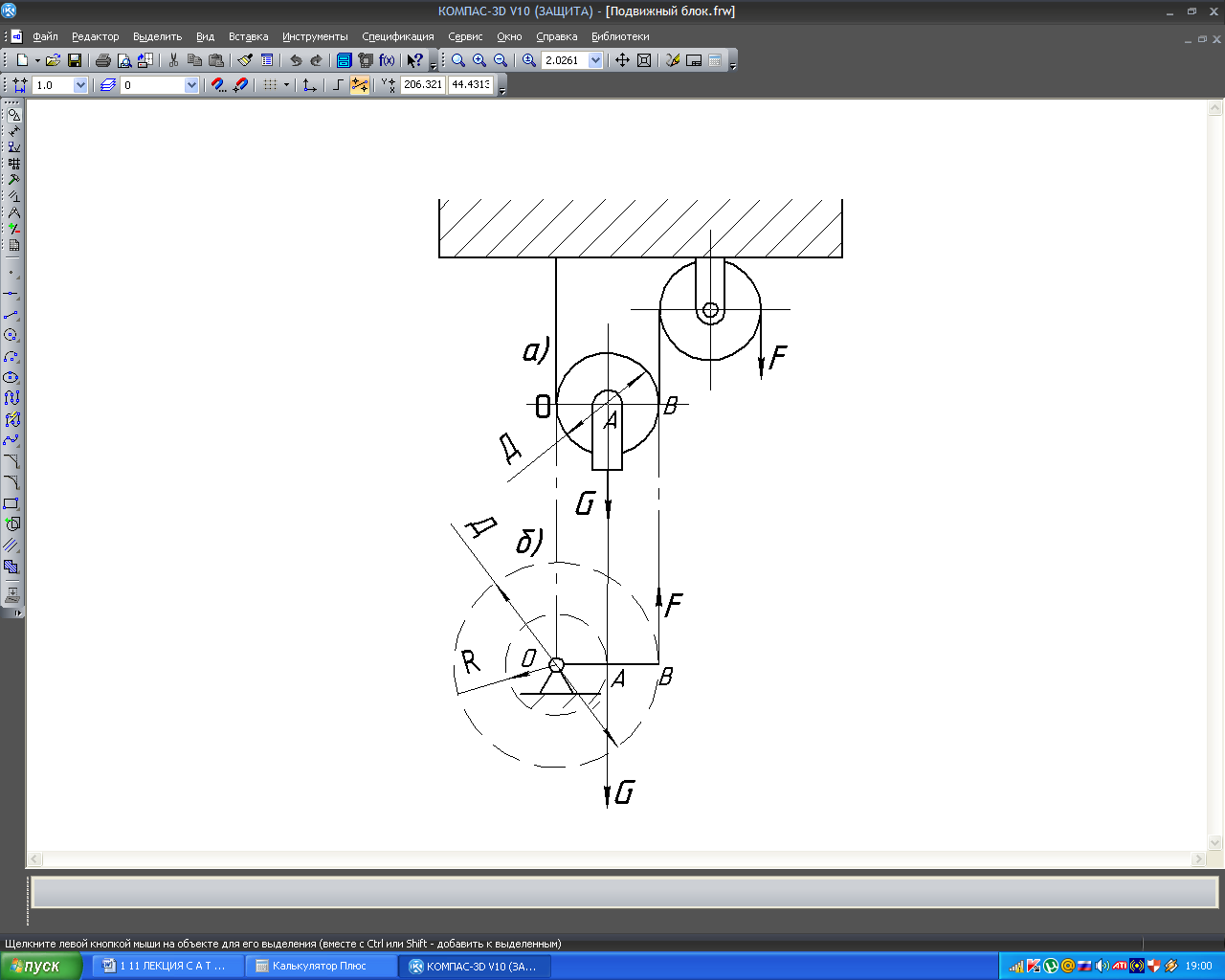 ример 6.2. Подъём груза G производится системой блоков, состоящей из подвижного и неподвижного блоков (рис.37,а). Подвижный блок подвешен на двух ветвях троса.

Т очкой опоры является точка О (рис.6.10,б). Вес груза уравновешивается силой F.

Составим уравнение равновесия сил:

-ОА∙G + ОВ×F = O.

ОА = R – Плечо силы G; ОВ = D- плечо силы F.

D∙F = R∙G;

Выигрыш в силе в два раза, но проигрываем в расстоянии в 2 раза т.е., например, если груз поднять на 1 м , то должны выбрать троса 2 м.

Рис.6.10

Тема 7. Плоская система произвольно расположенных сил

§ 10.1 Момент сил. Момент сил относительно точки

В реальных условиях к телу могут быть приложены силы, линии, действия которых не пересекаются в одной точке и не параллельны между собой. Исследование такой системы сил начинают с приведения сил к точке, лежащей в той же плоскости.

При закреплении тела в точке О сила F₁ стремится поворачивать его вокруг этой точки.

Точка, относительно которой тело получает вращение под действием силы, называется центром момента.

Кратчайшее расстояние от центра вращения тела до линии действия силы называется плечом силы.

Плечо силы численно равно длине перпендикуляра, опущенного из центра вращения на линию действия силы (Рис.7.1).

Произведение модуля силы на её плечо относительно точки вращения называется моментом силы.

М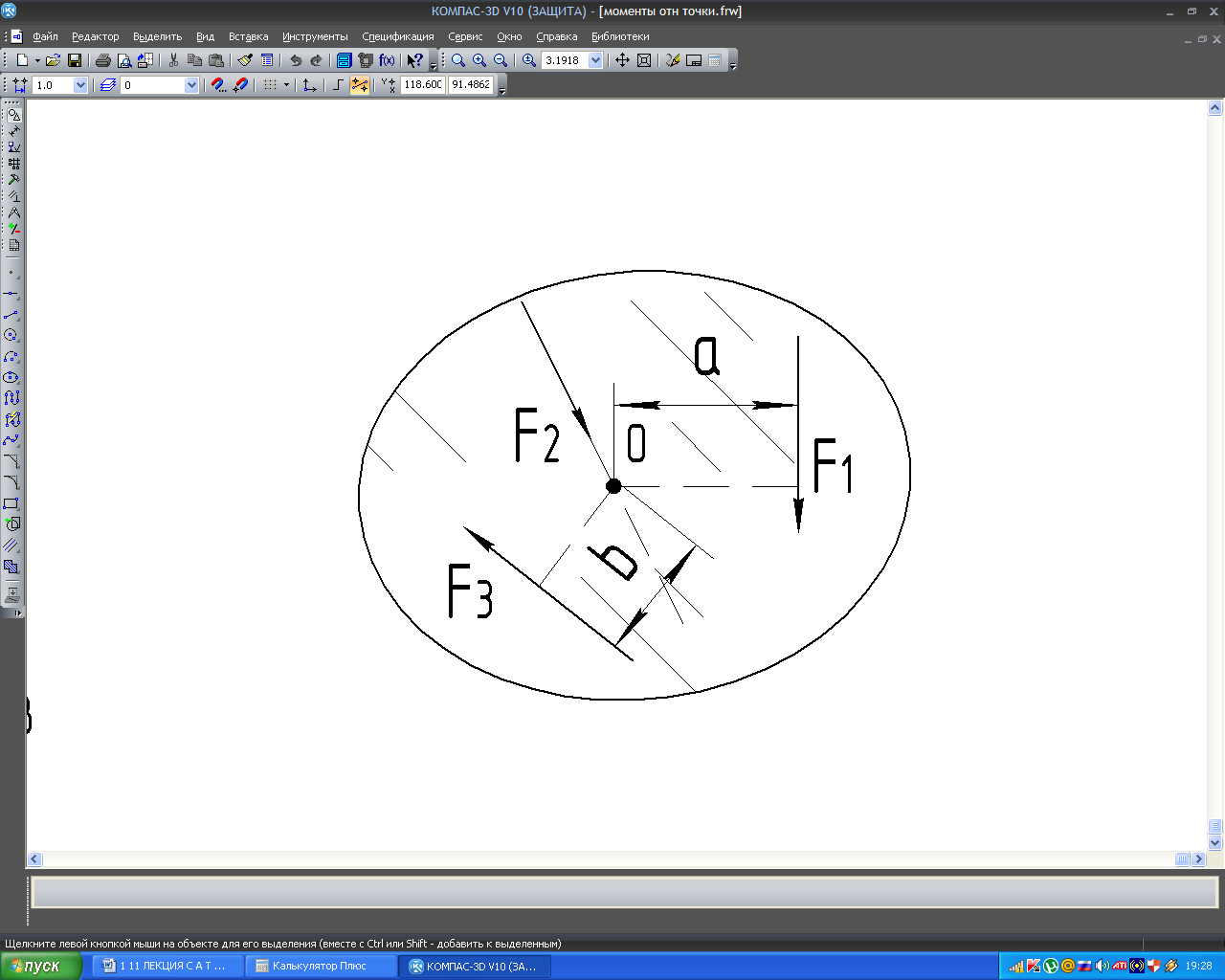 = F₁∙а.

Сила F₁ создаёт момент М₁ = F₁а; сила F₂ не создаёт момента М₂ = F₂0 = 0 – момент равен нулю, так как линия действия проходит через центр вращения тела (плечо силы отсутствует). Момент от силы F₃, М₃ = F₃b.

Рис.7.1