§ 6.3. Сложение пар

Если в одной плоскости действует несколько пар, то их можно заменить одной парой, момент которой равен суме моментов этих пар (рис.6.5).

Пусть на твёрдое тело в одной плоскости действуют две пары F₁ F'₁; F₂ F́′₂; F₁=3kH, F₂=4kH; h₁=300мм; h₂=400мм. Требуется определить равнодействующую пару, с плечём h= 200 мм.

Согласно, свойства эквивалентности пар заменим наши пары новыми парами, которые имеют общее плечо h=200мм.

М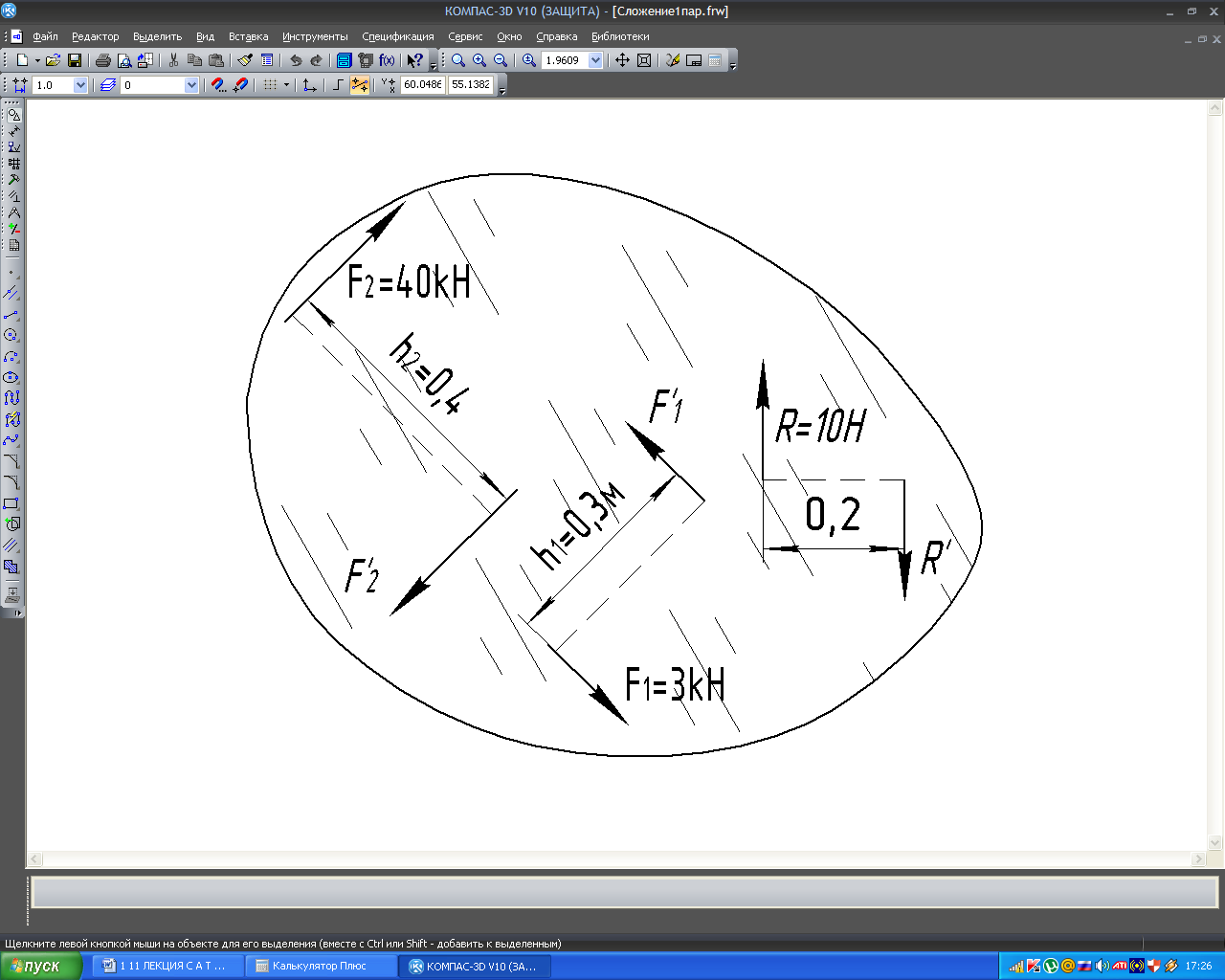 ₁=F₁·h₁=3·0,3=0,9 kH·м; М₂=F₂·h₂=4·0,4= 1,6 kH·м.

Определим модули сил с плечом h:

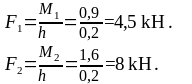
Модуль равнодействующей пары:

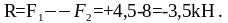
Рис.6.5

Вращение эквивалентной пары по часовой стрелке.

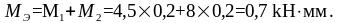
М_Э= R  h = 3,5 ∙ 0,2 = 0,7 kН·м.

Момент равнодействующей пары равен алгебраической сумме моментов слагаемых пар.

Если под действием нескольких пар твёрдое тело находится в равновесии, то такие пары при их сложений не дают равнодействующей пары, т.е. эти пары взаимно уравновешиваются. Отсюда следует вывод, что для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма моментов пар равнялась нулю.

Сумма проекций сил пары на любую ось равна нулю, поэтому пара сил не имеет равнодействующей.

Для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов данных пар равнялась нулю.

∑М_К = 0.

§ 6.4. Условия равновесия пар сил и моментов

Известно, что тело получает вращательное движение, если приложенные силы создают момент относительно возможной точки вращения. Если моменты сил, стремящиеся вращать тело в обратном направлении, окажутся равными моментам сил, то тело остаётся в равновесии.

Следовательно, для равновесия тела под действием пар сил и моментов необходимо, чтобы алгебраическая сумма моментов всех пар и моментов была равна нулю.

Пример 9.1. На 2х-колодочный тормоз действуют нормальные силы N=10кН (рис.6.6). Определить какой груз F может удерживать тормоз, если Д₁ =160 мм, Д₂ =250 мм. Коэффициент трения f=0,4.

К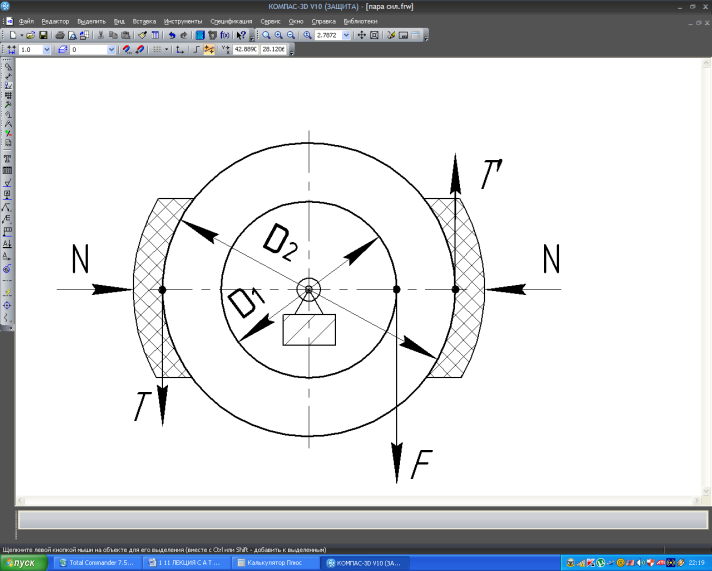 оэффициент трения f=Т/N.

Т-сила трения, N-нормальные силы, прижимающие колодки к барабану.

Сила трения Т=fN=0,4·10=4 kH.

Сила трения Т создаёт пару сил ТТ ':

М_Т = Т ∙ Д₂=4·0,25=1кН·м.

Рис.6.6

Уравнение равновесия:

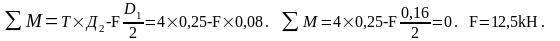
Пример 9.2. На концы консолей (консолью называется часть балки, выступающая за опору) балки (рис.6.7) действуют две параллельные силы

F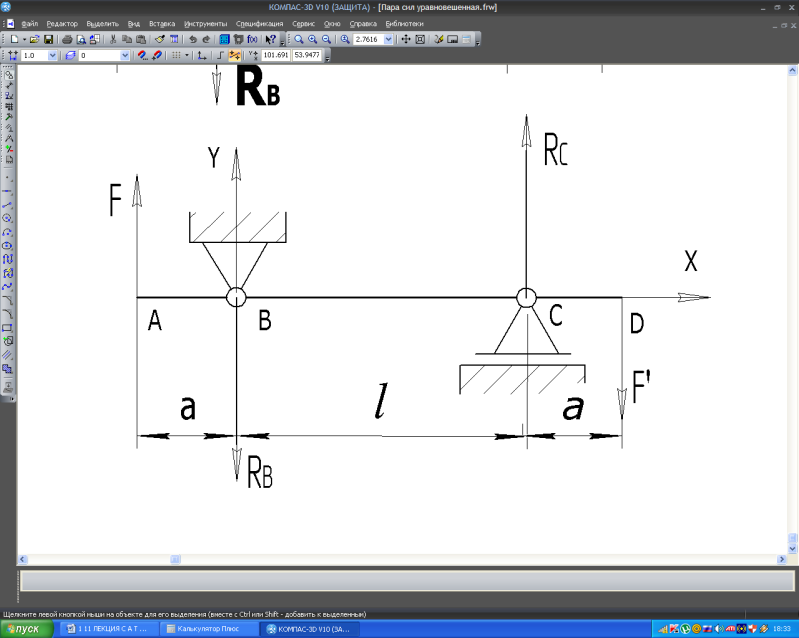 = F = 10кН, причём сила

F – направлена вверх, а сила F - вниз. Определить реакции опор балки, пренебрегая её весом, если пролёт балки l = 2 м и длина каждой консоли, а = 1 м.

На данную балку действует пара сил FF, стремящаяся повернуть балку по часовой стрелке.

Рис.6.7

Момент этой пары :М = -F(l +2a) = -104 = - 40 к∙Нм.

Пара сил создаёт давления на опоры В и С. Если убрать, например опору В, то мы должны приложить силу, равную силе давления и направленную в обратном направлении Rв. Эта сила называется реакцией связи или реакция опоры (более подробно будет рассматриваться ниже).

Пара сил может быть уравновешена парой, имеющий момент, равный по величине и обратный по знаку моменту данной пары.

Чтобы система сил находилась в равновесии, нужно пару сил уравновесить:

М + М_R = - F(2a+l) + (R_вl):2 = 104 - 202 = 0. R_B=R_C.